【题目】填空,完成下列说理过程
如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.
(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.

解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD=![]() ∠AOC.
∠AOC.
因为OE是∠BOC的平分线,
所以∠COE=![]() .
.
所以∠DOE=∠COD+ =![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
(2)由(1)可知
∠BOE=∠COE= ﹣∠COD= °.
所以∠AOE= ﹣∠BOE= °.
参考答案:
【答案】(1)∠BOC,∠COE,90;(2)∠DOE,25,∠AOB,155
【解析】
(1)首先根据角平分线定义可得∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,然后再根据角的和差关系可得答案;
∠BOC,然后再根据角的和差关系可得答案;
(2)首先计算出∠BOE的度数,再利用180°减去∠BOE的度数可得答案.
解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD=![]() ∠AOC.
∠AOC.
因为OE是∠BOC的平分线,
所以∠COE=![]() ∠BOC .
∠BOC .
所以∠DOE=∠COD+ ∠COE =![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= 90 °.
∠AOB= 90 °.
(2)由(1)可知
∠BOE=∠COE= ∠DOE ﹣∠COD= 25 °.
所以∠AOE= ∠AOB ﹣∠BOE= 155 °
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题发现:如图,已知:AB=AC,∠BAC=90°,直线m经过点A,过点B作BD⊥m于D, CE⊥m于E.我们把这种常见图形定义为“K”字图.很容易得到线段DE、BD、CE之间的数量关系是 .
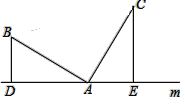
拓展探究:如图2,若AB=AC,∠BAC=∠BDA=∠AEC,则线段DE、BD、CE之间的数量关系还成立吗?如果成立,请证明之.
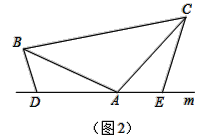
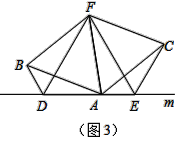
解决问题:如图3,若AB=AC,∠BAC=∠BDA=∠AEC=120°,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,BD=2,CE=4,求△DEF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,
 ,
, ,
, ,联结BD,若△BDC是等边三角形,那么梯形ABCD的面积是_________;
,联结BD,若△BDC是等边三角形,那么梯形ABCD的面积是_________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,
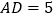 ,
, ,把矩形ABCD绕点A顺时针旋转,当点D落在射线CB上的点P处时,那么线段DP的长度等于_________.
,把矩形ABCD绕点A顺时针旋转,当点D落在射线CB上的点P处时,那么线段DP的长度等于_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,AB=4,∠C=30°,点E、F分别是边AB、CD的中点,作DP∥AB交EF于点G,∠PDC=90°,求线段GF的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民用水实行阶梯水价,实施细则如下表:
分档水量
年用水量 (立方米)
水价 (元/立方米)
第一阶梯
0~180(含)
5.00
第二阶梯
181~260(含)
7.00
第三阶梯
260以上
9.00
例如,某户家庭年使用自来水200 m3,应缴纳:180×5+(200-180)×7=1040元;
某户家庭年使用自来水300 m3,应缴纳:180×5+(260-180)×7+(300-260)×9=1820元.
(1)小刚家2017年共使用自来水170 m3,应缴纳 元;小刚家2018年共使用自来水260 m3,应缴纳 元.
(2)小强家2018年使用自来水共缴纳1180元,他家2018年共使用了多少自来水?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
 ,
,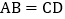 ,过点
,过点 ,垂足为
,垂足为 ,并延长
,并延长 ,使
,使 ,联结
,联结 .
.(1)求证:四边形
 是平行四边形。
是平行四边形。(2)联结
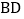 ,如果
,如果

相关试题

