【题目】问题发现:如图,已知:AB=AC,∠BAC=90°,直线m经过点A,过点B作BD⊥m于D, CE⊥m于E.我们把这种常见图形定义为“K”字图.很容易得到线段DE、BD、CE之间的数量关系是 .
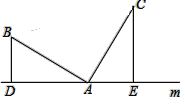
拓展探究:如图2,若AB=AC,∠BAC=∠BDA=∠AEC,则线段DE、BD、CE之间的数量关系还成立吗?如果成立,请证明之.
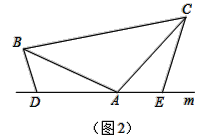
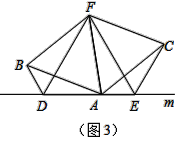
解决问题:如图3,若AB=AC,∠BAC=∠BDA=∠AEC=120°,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,BD=2,CE=4,求△DEF的周长.
参考答案:
【答案】(1)DE=BD+CE;(2)详见解析;(3)18.
【解析】
试题![]() 根据
根据![]() 得
得![]() 而
而![]() 根据等角的余角相等得
根据等角的余角相等得![]() 然后根据“AAS”可判断
然后根据“AAS”可判断![]() 则
则![]() 于是
于是![]()
(2)利用![]() 则
则![]() 得出
得出![]() 进而得出
进而得出![]() 即可得出答案;
即可得出答案;
(3)由![]() 和
和![]() 均为等边三角形,得到
均为等边三角形,得到![]() 利用
利用![]() 则
则![]() 得出
得出![]() 进而得出
进而得出![]() 根据全等三角形的性质得到,
根据全等三角形的性质得到,![]() 得到,
得到,![]() 根据全等三角形的性质得到
根据全等三角形的性质得到![]() 根据得到结论.
根据得到结论.
试题解析:证明:(1)∵BD⊥直线m,CE⊥直线m,
![]()
![]()
![]()
![]()
![]()
在△ADB和△CEA中,
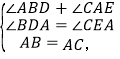
![]()
![]()
![]()
![]()
![]()
![]()
在△ADB和△CEA中,
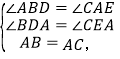
![]()
![]()
![]()
(3)∵△ABF和△ACF均为等边三角形,
![]()
![]()
![]()
![]()
在△ADB和△CEA中,
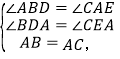
![]()
![]()
![]()
![]()
在△BDF与△AEF中,
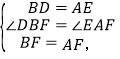
![]()
![]()
![]()
![]()
即![]()
![]() 是等边三角形.
是等边三角形.
![]()
![]() 的周长为:18.
的周长为:18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过A(﹣3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.

(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由. -
科目: 来源: 题型:
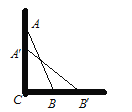
查看答案和解析>>【题目】一架长2.5米的梯子AB如图所示斜靠在一面墙上,这时梯足B离墙底C(∠C=90°)的距离BC为0.7米.
(1)求此时梯顶A距地面的高度AC;
(2)如果梯顶A下滑0.9米,那么梯足B在水平方向,向右滑动了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:如图所示是每一个小方格都是边长为1的正方形网格,
(1)利用网格线作图:
①在
 上找一点P,使点P到
上找一点P,使点P到 和
和 的距离相等;
的距离相等;②在射线
 上找一点Q,使
上找一点Q,使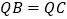 .
.(2)在(1)中连接
 与
与 ,试说明
,试说明 是直角三角形.
是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,
 ,
, ,
, ,联结BD,若△BDC是等边三角形,那么梯形ABCD的面积是_________;
,联结BD,若△BDC是等边三角形,那么梯形ABCD的面积是_________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,
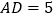 ,
, ,把矩形ABCD绕点A顺时针旋转,当点D落在射线CB上的点P处时,那么线段DP的长度等于_________.
,把矩形ABCD绕点A顺时针旋转,当点D落在射线CB上的点P处时,那么线段DP的长度等于_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空,完成下列说理过程
如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.
(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.

解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD=
 ∠AOC.
∠AOC.因为OE是∠BOC的平分线,
所以∠COE=
 .
.所以∠DOE=∠COD+ =
 (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ∠AOB= °.
∠AOB= °.(2)由(1)可知
∠BOE=∠COE= ﹣∠COD= °.
所以∠AOE= ﹣∠BOE= °.
相关试题

