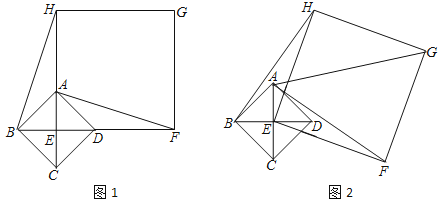
【题目】如图1,已知四边形ABCD是正方形,对角线AC、BD相交于点E,以点E为顶点作正方形EFGH.
(1)如图1,点A、D分别在EH和EF上,连接BH、AF,BH和AF有何数量关系,并说明理由;
(2)将正方形EFGH绕点E顺时针方向旋转,如图2,判断BH和AF的数量关系,并说明理由.
参考答案:
【答案】(1)BH=AF,见解析;(2)BH=AF,见解析.
【解析】
(1)根据正方形的性质可得AE=BE,∠BEH=∠AEF=90°,然后利用“边角边”证明△BEH和△AEF全等,根据全等三角形对应边相等即可得证;
(2)根据正方形的性质得到AE=BE,∠BEA=90°,EF=EH,∠HEF=90°,然后利用“边角边”证明△BEH和△AEF全等,根据全等三角形的性质即可得到结论.
(1)BH=AF,理由如下:
在正方形ABCD中,AE=BE,∠BEH=∠AEF=90°,
∵四边形EFGH是正方形,
∴EF=EH,
在△BEH和△AEF中,
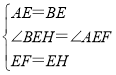 ,
,
∴△BEH≌△AEF(SAS),
∴BH=AF;
(2)BH=AF,理由如下:
∵四边形ABCD是正方形,
∴AE=BE,∠BEA=90°,
∵四边形EFGH是正方形,
∴EF=EH,∠HEF=90°,
∴∠BEA+∠AEH=∠HEF+∠AEH,
即∠BEH=∠AEF,
在△BEH与△AEF中,
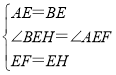 ,
,
∴△BEH≌△AEF(SAS),
∴BH=AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某演唱会购买门票的方式有两种.
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;
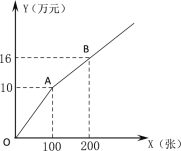
方式二:如图所示.
设购买门票x张,总费用为y万元,方式一中:总费用=广告赞助费+门票费.
(1)求方式一中y与x的函数关系式.
(2)若甲、乙两个单位分别采用方式一、方式二购买本场演唱会门票共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
-
科目: 来源: 题型:
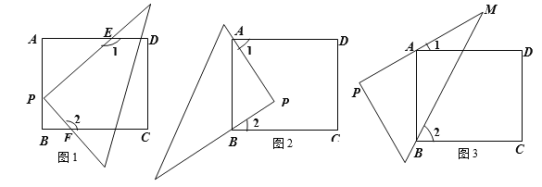
查看答案和解析>>【题目】操作:将一个含30°角的直角三角形放在一长方形纸片上,
(1)如图1所示,直角顶点P在长方形的边AB上,直角边交长方形的两边AD、BC于点E、F,如果图中的∠1=140°,那么∠2= 度.
(2)如图2所示,直角顶点P在长方形内,且长方形的顶点A、B在∠P的直角边上,那么图中的∠1与∠2会有怎样的关系?为什么?
(3)如果将30°角如图3摆放,使得长方形的顶点A、B在30°角的两边上,此时,你认为图中的∠1与∠2会有怎样的关系?请直接写出你的结论: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是( )
A. 第一次向右拐40, 第二次向左拐140
B. 第一次向左拐40, 第二次向右拐40
C. 第一次向左拐40, 第二次向左拐140
D. 第一次向右拐40, 第二次向右拐40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为九年级数学竞赛获奖选手购买以下三种奖品,其中小笔记本每本5元,大笔记本每本7元,钢笔每支10元,购买的大笔记本的数量是钢笔数量的2倍,共花费346元,若使购买的奖品总数最多,则这三种奖品的购买数量各为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=x+n﹣2与直线l2:y=mx+n相交于点P(1,2).
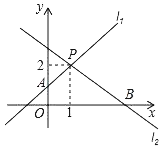
(1)求m,n的值;
(2)请结合图象直接写出不等式mx+n>x+n﹣2的解集.
(3)若直线l1与y轴交于点A,直线l2与x轴交于点B,求四边形PAOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列说法中不正确的是( )

A. ∠1与∠AOB是同一个角B. ∠AOC也可以用∠O表示
C. ∠β=∠BOCD. 图中有三个角
相关试题

