【题目】操作:将一个含30°角的直角三角形放在一长方形纸片上,
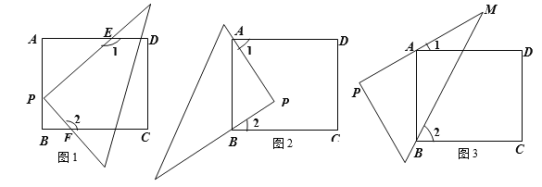
(1)如图1所示,直角顶点P在长方形的边AB上,直角边交长方形的两边AD、BC于点E、F,如果图中的∠1=140°,那么∠2= 度.
(2)如图2所示,直角顶点P在长方形内,且长方形的顶点A、B在∠P的直角边上,那么图中的∠1与∠2会有怎样的关系?为什么?
(3)如果将30°角如图3摆放,使得长方形的顶点A、B在30°角的两边上,此时,你认为图中的∠1与∠2会有怎样的关系?请直接写出你的结论: .
参考答案:
【答案】130°;互余;∠2=∠1+30°
【解析】
本题考查的是平行线的性质和长方形的性质以及多边形内角和,运用多边形内角和与两线平行同旁内角互补即可解答第(1);利用两直线平行,同旁内角互补,结合图形即可求出(2);利用两直线平行,内错角相等即可求出(3)
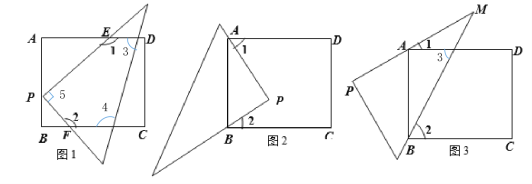
(1)如图1,因为∠1+∠2+∠3+∠4+∠5=540°(多边形内角和定理),∠3+∠4=180°(两直线平行同旁内角互补),∠5=90°,所以∠1+∠2=270°,因为∠1=140°,所以∠2=130°;
(2)因为AD∥BC,所以∠DAB+∠CBA=180°,因为∠P=90°,所以∠PAB+∠PBA=90°,所以∠1+∠2=(∠DAB+∠CBA)-(∠PAB+∠PBA)=90°,即∠1与∠2互余;
(3)因为AD∥BC,所以∠2=∠3,因为∠3=∠1+∠M,即∠3=∠1+30°,所以∠2=∠1+30°
-
科目: 来源: 题型:
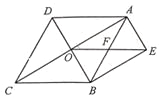
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
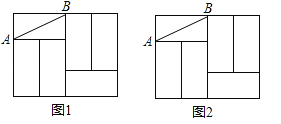
(1)在图1中画出一个45°角,使点A或点B是这个角的顶点,且AB为这个角的一边;
(2)在图2中画出线段AB的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某演唱会购买门票的方式有两种.
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;
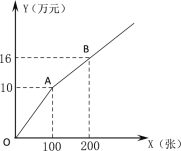
方式二:如图所示.
设购买门票x张,总费用为y万元,方式一中:总费用=广告赞助费+门票费.
(1)求方式一中y与x的函数关系式.
(2)若甲、乙两个单位分别采用方式一、方式二购买本场演唱会门票共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是( )
A. 第一次向右拐40, 第二次向左拐140
B. 第一次向左拐40, 第二次向右拐40
C. 第一次向左拐40, 第二次向左拐140
D. 第一次向右拐40, 第二次向右拐40°
-
科目: 来源: 题型:
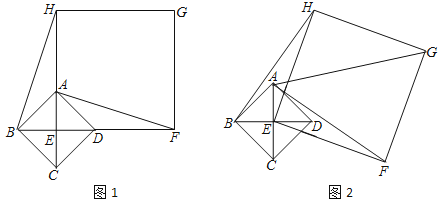
查看答案和解析>>【题目】如图1,已知四边形ABCD是正方形,对角线AC、BD相交于点E,以点E为顶点作正方形EFGH.
(1)如图1,点A、D分别在EH和EF上,连接BH、AF,BH和AF有何数量关系,并说明理由;
(2)将正方形EFGH绕点E顺时针方向旋转,如图2,判断BH和AF的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为九年级数学竞赛获奖选手购买以下三种奖品,其中小笔记本每本5元,大笔记本每本7元,钢笔每支10元,购买的大笔记本的数量是钢笔数量的2倍,共花费346元,若使购买的奖品总数最多,则这三种奖品的购买数量各为多少?
相关试题

