【题目】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2.求:四边形ABCD的面积. 
参考答案:
【答案】解:延长AD,BC,交于点E,
在Rt△ABE中,∠A=60°,AB=4,
∴∠E=30°,AE=2AB=8,
∴BE= ![]() =4
=4 ![]() ,
,
在Rt△DCE中,∠E=30°,CD=2,
∴CE=2CD=4,根据勾股定理得:DE= ![]() =2
=2 ![]() ,
,
则S四边形ABCD=S△ABE﹣S△DCE= ![]() ABBE﹣
ABBE﹣ ![]() DCED=8
DCED=8 ![]() ﹣2
﹣2 ![]() =6
=6 ![]() .
.
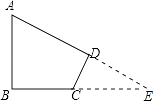
【解析】延长AD,BC,交于点E,在直角三角形ABE中,利用30度角所对的直角边得到AE=2AB,再利用勾股定理求出BE的长,在直角三角形DCE中,同理求出DE的长,四边形ABCD面积=三角形ABE面积﹣三角形DCE面积,求出即可.
【考点精析】关于本题考查的含30度角的直角三角形和勾股定理的概念,需要了解在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在一次大课间活动中,采用了四钟活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图.
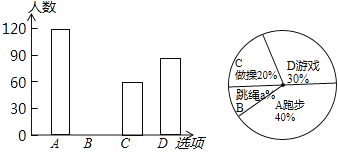
请结合统计图,回答下列问题:
(1)本次调查学生共 人,a= ,并将条形图补充完整;
(2)如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?
(3)学校让每班在A、B、C、D四钟活动形式中,随机抽取两种开展活动,请用树状图或列表的方法,求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列多项式分解因式
(1)12xy2-3x3;
(2)(x-2)(x-4)+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1,0),B(x2,0)(0<x1<x2)两点,与y轴交于点C.
(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;
(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;
(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条数轴由点A处对折,表示﹣30的数的点恰好与表示4的数的点重合,则点A表示的数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E、F在四边形ABCD的对角线延长线上,AE=CF,DE∥BF,∠1=∠2.
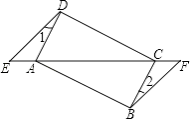
(1)求证:△AED≌△CFB;
(2)若AD⊥CD,四边形ABCD是什么特殊四边形?请说明理由. -
科目: 来源: 题型:
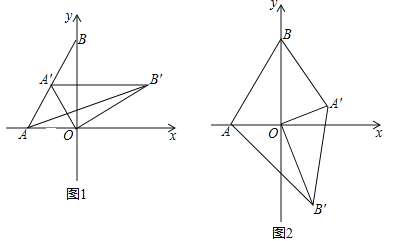
查看答案和解析>>【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0,
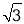 ).
).(1)求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1,△BA′O的面积为S2,S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
相关试题

