【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1,0),B(x2,0)(0<x1<x2)两点,与y轴交于点C.
(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;
(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;
(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.
参考答案:
【答案】(1)y=4x2﹣16x+12;(2)P(![]() ,﹣3).(3)不存在.理由见解析.
,﹣3).(3)不存在.理由见解析.
【解析】
试题分析:(1)由tan∠ABC=4,可设B(m,0),则A(m-2,0),C(0,4m),可得抛物线的解析式为y=4(x-m)(x-m+2),把C点坐标代入即可求解;
(2)设P(m,4m2-16m+12).作PH∥OC交BC于H,根据SΔPBC=SΔPHC+SΔPHB,构建二次函数,求解即可;
(3)不存在.假设存在,由题意知,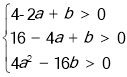 且1<﹣
且1<﹣![]() <2,求出a的值,解不等式组即可得解.
<2,求出a的值,解不等式组即可得解.
试题解析:(1)∵tan∠ABC=4
∴可以假设B(m,0),则A(m﹣2,0),C(0,4m),
∴可以假设抛物线的解析式为y=4(x﹣m)(x﹣m+2),
把C(0,4m)代入y=4(x﹣m)(x﹣m+2),得m=3,
∴抛物线的解析式为y=4(x﹣3)(x﹣1),
∴y=4x2﹣16x+12,
(2)如图,设P(m,4m2﹣16m+12).作PH∥OC交BC于H.
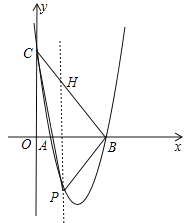
∵B(3,0),C(0,12),
∴直线BC的解析式为y=﹣4x+12,
∴H(m,﹣4m+12),
∴S△PBC=S△PHC+S△PHB=![]() (﹣4m+12﹣4m2+16m﹣12)3=﹣6(m﹣
(﹣4m+12﹣4m2+16m﹣12)3=﹣6(m﹣![]() )2+
)2+![]() ,
,
∵﹣6<0,
∴m=![]() 时,△PBC面积最大,
时,△PBC面积最大,
此时P(![]() ,﹣3).
,﹣3).
(3)不存在.
理由:假设存在.由题意可知,
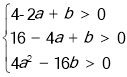 且1<﹣
且1<﹣![]() <2,
<2,
∴4<a<8,
∵a是整数,
∴a=5 或6或7,
当a=5时,代入不等式组,不等式组无解.
当a=6时,代入不等式组,不等式组无解.
当a=7时,代入不等式组,不等式组无解.
综上所述,不存在整数a、b,使得1<x1<2和1<x2<2同时成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决老百姓看病贵的问题,对某种原价为400元的药品进行连续两次降价,降价后的价格为256元,设每次降价的百分率为x,则依题意列方程为: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在一次大课间活动中,采用了四钟活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图.
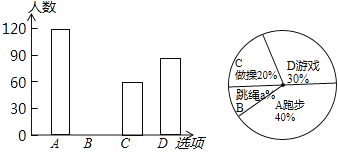
请结合统计图,回答下列问题:
(1)本次调查学生共 人,a= ,并将条形图补充完整;
(2)如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?
(3)学校让每班在A、B、C、D四钟活动形式中,随机抽取两种开展活动,请用树状图或列表的方法,求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列多项式分解因式
(1)12xy2-3x3;
(2)(x-2)(x-4)+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2.求:四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一条数轴由点A处对折,表示﹣30的数的点恰好与表示4的数的点重合,则点A表示的数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E、F在四边形ABCD的对角线延长线上,AE=CF,DE∥BF,∠1=∠2.
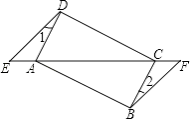
(1)求证:△AED≌△CFB;
(2)若AD⊥CD,四边形ABCD是什么特殊四边形?请说明理由.
相关试题

