【题目】如图,已知点E、F在四边形ABCD的对角线延长线上,AE=CF,DE∥BF,∠1=∠2.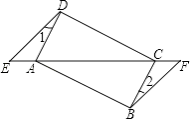
(1)求证:△AED≌△CFB;
(2)若AD⊥CD,四边形ABCD是什么特殊四边形?请说明理由.
参考答案:
【答案】
(1)证明:∵DE∥BF,
∴∠E=∠F,
在△AED和△CFB中,
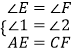 ,
,
∴△AED≌△CFB(AAS)
(2)解:四边形ABCD是矩形.
理由如下:∵△AED≌△CFB,
∴AD=BC,∠DAE=∠BCF,
∴∠DAC=∠BCA,
∴AD∥BC,
∴四边形ABCD是平行四边形,
又∵AD⊥CD,
∴四边形ABCD是矩形.
【解析】(1)利用两直线平行,内错角相等可得一组对应角相等,结合已知条件,运用角角边证得全等;(2)利用(1)的结论,可证得平行四边形,再结合已知条件AD⊥CD,可证得矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1,0),B(x2,0)(0<x1<x2)两点,与y轴交于点C.
(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;
(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;
(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2.求:四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一条数轴由点A处对折,表示﹣30的数的点恰好与表示4的数的点重合,则点A表示的数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0,
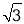 ).
).(1)求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1,△BA′O的面积为S2,S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
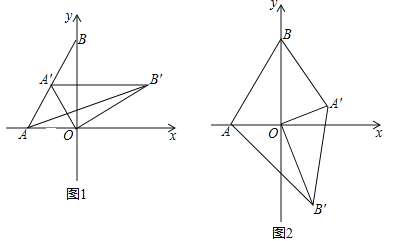
-
科目: 来源: 题型:
查看答案和解析>>【题目】【探究函数y=x+
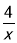 的图象与性质】
的图象与性质】(1)函数y=x+
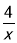 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;(2)下列四个函数图象中函数y=x+
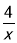 的图象大致是 ;
的图象大致是 ;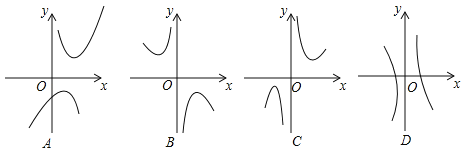
(3)对于函数y=x+
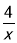 ,求当x>0时,y的取值范围.
,求当x>0时,y的取值范围.请将下列的求解过程补充完整.
解:∵x>0
∴y=x+
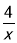 =(
=(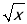 )2+(
)2+(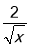 )2=(
)2=(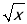 ﹣
﹣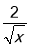 )2+
)2+ ∵(
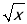 ﹣
﹣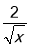 )2≥0
)2≥0∴y≥ .
[拓展运用]
(4)若函数y=
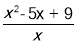 ,则y的取值范围 .
,则y的取值范围 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
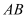 是⊙
是⊙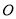 的直径,
的直径,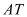 是⊙
是⊙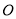 的切线,
的切线,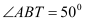 ,
,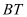 交⊙
交⊙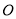 于点
于点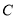 ,
,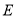 是
是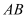 上一点,延长
上一点,延长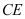 交⊙
交⊙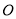 于点
于点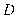 .
.(1)如图①,求
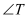 和
和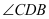 的大小;
的大小;(2)如图②,当
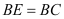 时,求
时,求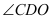 的大小.
的大小.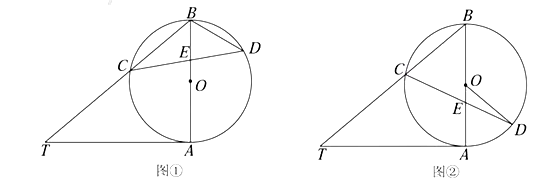
相关试题

