【题目】如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.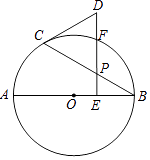
(1)求证:DC是⊙O的切线;
(2)若∠CBA=30°,射线EP交⊙O于点 F,当点 F恰好是弧BC的中点时,判断以B,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
参考答案:
【答案】
(1)证明:连接OC,

∵DP=DC,
∴∠DPC=∠DCP,
∵∠DPC=∠BPE,
∴∠BPE=∠DCP,
∵PE⊥AB,
∴∠BEP=90°,
∴∠B+∠APE=90°,
∵OB=OC,
∴∠OCB=∠B,
∴∠OCB+∠DCP=90°,
∴OC⊥CD,
∴直线CD与⊙O相切
(2)解:以B、O、C、F为顶点的四边形是菱形,理由如下:
连接AC,
∵∠CBA=30°,
∴∠A=60°,
∴△OAC为等边三角形,
∴∠BOC=120°,
连接OF,BF,CF
∵F是弧BC的中点,
∴∠BOF=∠COF=60°,
∴△BOF与△COF均为等边三角形,
∴BF=BO=OC=CF,
∴四边形BOCF为菱形.
【解析】(1)连接OC,然后依据已知条件和圆的基本性质证明OC⊥CD,最后,依据切线的判定定理进行证明即可;
(2)连接AC,由∠CAB=30°可证明△OAC为等边三角形,于是可得到∠BOC=120°,由F是弧AC的中点,易证明△BOF、△COF均为等边三角形,依据等边三角形的性质可得到BF=BO=OC=CF,从而可证明四边形BOCF为菱形.
【考点精析】根据题目的已知条件,利用菱形的判定方法的相关知识可以得到问题的答案,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民节水意识,合理利用水资源,某市采用价格调控手段达到节约用水的目的,规定:每户居民每月用水不超过15m3时,按基本价格收费;超过15m3时,不超过的部分仍按基本价格收费,超过的部分要加价收费,该市某户居民今年4、5月份的用水量和水费如表所示:
月份
用水量/m3
水费/元
4
16
50
5
20
70
(1)求该市居民用水的两种收费价格;
(2)若该居民6月份交水费80元,那么该居民这个月水量为m3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DCB中,∠A=∠D=72°,∠ACB=∠DBC=36°,则图中等腰三角形的个数是( )
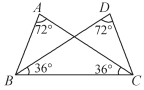
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,边长为2的正方形ABCD中,点P在AB边上(不与点A、B重合),点Q在BC边上(不与点B、C重合)
第一次操作:将线段PQ绕点Q顺时针旋转,当点P落在正方形上时,记为点M;
第二次操作:将线段QM绕点M顺时针旋转,当点Q落在正方形上时,记为点N;
依次操作下去…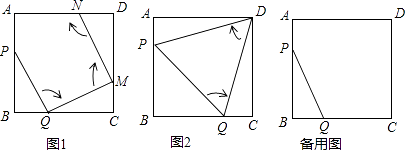
(1)如图2,经过两次操作后得到△PQD、△PQD的形状是 , 求此时线段PQ的长 ;
(2)若经过三次操作可得到四边形PQMN.
①请直接判断四边形PQMN的形状,直接写出此时此刻AP与BQ的数量关系;
②以①中的结论为前提,直接写出四边形PQMN的面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值:
①(x﹣1)(x+1)=x2﹣1;
②(x﹣1)(x2+x+1)=x3﹣1;
③(x﹣1)(x3+x2+x+1)=x4﹣1;
…
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)= .
请你利用上面的结论,再完成下面两题的计算:
(1)210+29+28+…+2+1
(2)3n+3n-1+3n-2…+3+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据6,3,4,7,6,3,5,6,求:
(1)这组数据的平均数、众数、中位数;
(2)这组数据的方差和标准差.
相关试题

