【题目】为了加强公民节水意识,合理利用水资源,某市采用价格调控手段达到节约用水的目的,规定:每户居民每月用水不超过15m3时,按基本价格收费;超过15m3时,不超过的部分仍按基本价格收费,超过的部分要加价收费,该市某户居民今年4、5月份的用水量和水费如表所示:
月份 | 用水量/m3 | 水费/元 |
4 | 16 | 50 |
5 | 20 | 70 |
(1)求该市居民用水的两种收费价格;
(2)若该居民6月份交水费80元,那么该居民这个月水量为m3 .
参考答案:
【答案】
(1)解:设基本水费价格为:x元/m3,超过的部分水费价格为:y元/m3,
![]() ,
,
解得: ![]() ,
,
答:基本水费价格为:3元/m3,超过的部分水费价格为:5元/m3
(2)22
【解析】解:(1)解:设基本水费价格为:x元/m3,超过的部分水费价格为:y元/m3,
![]() ,
,
解得: ![]() ,
,
答:基本水费价格为:3元/m3,超过的部分水费价格为:5元/m3
(2)∵3×15=45<80(元),
∴这个月一定超过15立方米,
则15×2+5(a﹣15)=80,
解得:x=22.
答:这个月该用户用水22立方米.
所以答案是:(1)基本水费价格为:3元/m3,超过的部分水费价格为:5元/m3;(2)22.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=
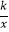 (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).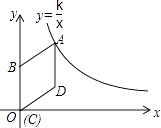
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=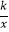 (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为
 秒,当
秒,当 为何值时,直线EF平分∠AOB?
为何值时,直线EF平分∠AOB?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DCB中,∠A=∠D=72°,∠ACB=∠DBC=36°,则图中等腰三角形的个数是( )
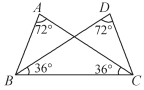
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.
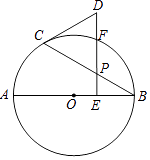
(1)求证:DC是⊙O的切线;
(2)若∠CBA=30°,射线EP交⊙O于点 F,当点 F恰好是弧BC的中点时,判断以B,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
相关试题

