【题目】如图1,边长为2的正方形ABCD中,点P在AB边上(不与点A、B重合),点Q在BC边上(不与点B、C重合)
第一次操作:将线段PQ绕点Q顺时针旋转,当点P落在正方形上时,记为点M;
第二次操作:将线段QM绕点M顺时针旋转,当点Q落在正方形上时,记为点N;
依次操作下去…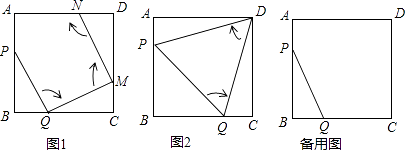
(1)如图2,经过两次操作后得到△PQD、△PQD的形状是 , 求此时线段PQ的长 ;
(2)若经过三次操作可得到四边形PQMN.
①请直接判断四边形PQMN的形状,直接写出此时此刻AP与BQ的数量关系;
②以①中的结论为前提,直接写出四边形PQMN的面积的取值范围.
参考答案:
【答案】
(1)等边三角形,解:由旋转得:DP=PQ=DQ,∴△PQD的形状为等边三角形,∵四边形ABCD是正方形,∴AD=CD=BC=AB,∠A=∠B=∠C=90°,∵DP=DQ,∴Rt△ADP≌Rt△CDQ,∴AP=CQ,∴BP=BQ,∴△BPQ是等腰直角三角形,设BP的长为x,则PQ= ![]() x,∴AP=2﹣x,∵在Rt△ADP中,DP2=AD2+AP2,DP=PQ,∴(
x,∴AP=2﹣x,∵在Rt△ADP中,DP2=AD2+AP2,DP=PQ,∴( ![]() x)2=22+(2﹣x)2,∴x2+4x﹣8=0,解得:x1=﹣2+2
x)2=22+(2﹣x)2,∴x2+4x﹣8=0,解得:x1=﹣2+2 ![]() ,x2=﹣2﹣2
,x2=﹣2﹣2 ![]() (不合题意,舍去),∵PQ=
(不合题意,舍去),∵PQ= ![]() x=
x= ![]() (﹣2+2
(﹣2+2 ![]() )=﹣2
)=﹣2 ![]() +2
+2 ![]() ;
;
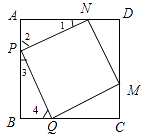
(2)解:①四边形PQMN的形状为正方形,此时AP=BQ.理由如下:
如图所示:
由旋转性质可知,PQ=QM=MN=NP,
∴四边形PQMN是菱形,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
∵∠3+∠4=90°,∠2+∠3=90°,
∴∠QPN=90°,∠2=∠4.
∴四边形PQMN是正方形;
在△APN和△BQP中, 
∴△APN≌△BQP(AAS)
∴AP=BQ.
②利用①中结论得:△APN、△BQP、△CMQ、△DNM均为全等三角形,
∴BQ=CM=DN=AP=x,AN=BP=CQ=DM=2﹣x.
∴四边形PQMN的面积S=S正方形ABCD﹣4S△APN=2×2﹣4× ![]() x(2﹣x)=2x2﹣4x+4,
x(2﹣x)=2x2﹣4x+4,
∴S=2x2﹣4x+4(0<x<2),
∵y=2(x﹣1)2+2,
∴当x=1时,S有最小值2;
当x=0时,S=4,
∴四边形PQMN的面积S取值范围是2≤S<4.
【解析】(1)根据HL证明Rt△ADP≌Rt△CDQ,得AP=CQ,所以△BPQ是等腰直角三角形,设BP的长为x,则PQ= ![]() x,根据勾股定理列方程,解方程即可得PQ的长;(2)①由旋转性质可知,PQ=QM=MN=NP,求出四边形PQMN是菱形,再证出∠QPN=90°,得出四边形PQMN是正方形;由AAS证明△APN≌△BQP,得出AP=BQ即可.②利用①中结论得:△APN、△BQP、△CMQ、△DNM均为全等三角形,得出BQ=CM=DN=AP=x,AN=BP=CQ=DM=2﹣x.四边形PQMN的面积S=S正方形ABCD﹣4S△APN=2x2﹣4x+4,由二次函数的性质即可得出答案.
x,根据勾股定理列方程,解方程即可得PQ的长;(2)①由旋转性质可知,PQ=QM=MN=NP,求出四边形PQMN是菱形,再证出∠QPN=90°,得出四边形PQMN是正方形;由AAS证明△APN≌△BQP,得出AP=BQ即可.②利用①中结论得:△APN、△BQP、△CMQ、△DNM均为全等三角形,得出BQ=CM=DN=AP=x,AN=BP=CQ=DM=2﹣x.四边形PQMN的面积S=S正方形ABCD﹣4S△APN=2x2﹣4x+4,由二次函数的性质即可得出答案.
【考点精析】认真审题,首先需要了解旋转的性质(①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DCB中,∠A=∠D=72°,∠ACB=∠DBC=36°,则图中等腰三角形的个数是( )
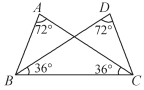
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.
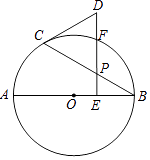
(1)求证:DC是⊙O的切线;
(2)若∠CBA=30°,射线EP交⊙O于点 F,当点 F恰好是弧BC的中点时,判断以B,O,C,F为顶点的四边形是什么特殊四边形?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值:
①(x﹣1)(x+1)=x2﹣1;
②(x﹣1)(x2+x+1)=x3﹣1;
③(x﹣1)(x3+x2+x+1)=x4﹣1;
…
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)= .
请你利用上面的结论,再完成下面两题的计算:
(1)210+29+28+…+2+1
(2)3n+3n-1+3n-2…+3+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据6,3,4,7,6,3,5,6,求:
(1)这组数据的平均数、众数、中位数;
(2)这组数据的方差和标准差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小聪是一名非常爱钻研的七年级学生,他将4块完全一样的三角板(如图1)拼成了一个非常工整的图形(如图2),请教老师以后得知:该图形是一个正方形,并且里面的四边形也是一个正方形,为了作进一步的探究,小明将三角板的三边长用
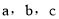 表示(如图3),将两个正方形分别用正方形ABCD和正方形EFGH表示,然后他用两种不用的方法计算了正方形ABCD的面积.
表示(如图3),将两个正方形分别用正方形ABCD和正方形EFGH表示,然后他用两种不用的方法计算了正方形ABCD的面积.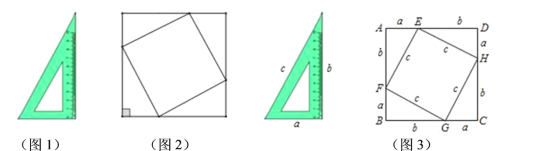
(1)请你用两种不同的方法计算出正方形ABCD的面积;
方法一: .
方法二: .
(2)根据(1)的计算结果,你能得到怎么样的结论?
(3)请用文字语言描述(2)中的结论.
相关试题

