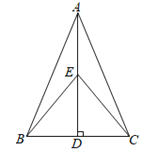
【题目】如图,在等腰△ABC中,AD是底边BC边上的高,点E是AD上的一点.
(1)求证:△BEC是等腰三角形.
(2)若AB=AC=13,BC=10,点E是AD的中点,求BE的长.
参考答案:
【答案】(1)证明见解析; (2)![]()
【解析】试题分析:
(1)根据等腰三角形的性质,AD是BC的垂直平分线,则EB=EC.
(2)由“三线合一”求得BD的长,在直角三角形ABD中,由勾股定理得到AD的长,从而求得DE,再由勾股定理求BE.
试题解析:
(1)因为AB=AC,AD⊥BC,所以BD=BC,所以EB=EC.
所以△BEC是等腰三角形.
(2)因为AB=AC,AD⊥BC,所以BD=5.
在Rt△ABD中,由勾股定理可得AD=12.
因为E是AD的中点,所以DE=6.
在Rt△BDE中,由勾股定理得:BE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】世界文化遗产长城总长约为6700000m,若将6700000用科学记数法表示为6.7×10n(n是正整数),则n的值为
A.5 B.6 C.7 D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】与﹣2的和为0的数是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣20+(﹣14)﹣(﹣18)﹣13
(2)﹣4÷ ﹣(﹣
﹣(﹣  )×(﹣30)
)×(﹣30)
(3)﹣22+|5﹣8|+24÷(﹣3)×
(4)( ﹣
﹣  ﹣
﹣  )×24÷(﹣2)3 .
)×24÷(﹣2)3 . -
科目: 来源: 题型:
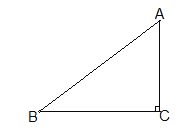
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t秒(t>0).
(1)若点P在BC上,且满足PA=PB,求此时t的值;
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
(3)在运动过程中,当t为何值时,△ACP为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简下列各题
(1)-2a2b-3ab2+3a2b-4ab2;
(2)2(xyz-3x)+5(2x-3xyz);
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AD=2,∠A=60°,BC=
 ,CD=3.
,CD=3.(1)求∠ADC的度数;
(2)求四边形ABCD的面积.

相关试题

