搜索
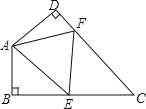
【题目】如图，在四边形ABCD中，∠C=50°，∠B=∠D=90°，E，F分别是BC，DC上的点，当△AEF的周长最小时，∠EAF=________度。
参考答案：
【答案】80°
【解析】
据要使△AEF的周长最小，即利用点的对称，使三角形的三边在同一直线上，作出A关于BC和CD的对称点A′，A″，即可得出∠A′+∠A″=∠HAA′=50°，进而得出∠EAB+∠FAD=50°，即可得出答案．
解：作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于E，交CD于F，则A′A″即为△AEF的周长最小值．作DA延长线AH，
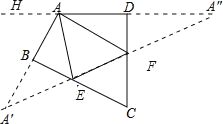
∵∠C=50°，
∴∠DAB=130°，
∴∠HAA′=50°，
∴∠A′+∠A″=∠HAA′=50°，
∵∠A′=∠EAB，∠A″=∠FAD，
∴∠EAB+∠FAD=50°，
∴∠EAF=130°-50°=80°，
故答案为：80°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了看一种图钉落地后钉尖着地的概率有多大，小明作了
次试验，其中钉尖着地的次数是
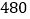次．下列说法错误的是（ ）A. 钉尖着地的频率是
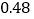
B. 前
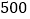次试验结束后，钉尖着地的次数一定是
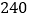次C. 钉尖着地的概率大约是
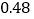
D. 随着试验次数的增加，钉尖着地的频率稳定在
-
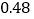
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，点B、F、C、E在同一直线上，AC、DF相交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AC=DF，BF=EC．求证：
（1）△ABC≌△DEF；
（2）FG=CG．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图，已知∠MAN＝120°，AC平分∠MAN，∠ABC＝∠ADC＝90°，则能得到如下两个结论：①DC＝BC；②AD+AB＝AC． 请你证明结论②．
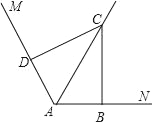
（2）如图，把（1）中的条件“∠ABC＝∠ADC＝90°”改为∠ABC+∠ADC＝180°，其他条件不变，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．
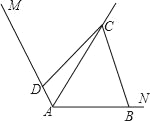
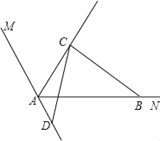
（3）如图3，如果D在AM的反向延长线上，把（1）中的条件“∠ABC＝∠ADC＝90°”改为∠ABC＝∠ADC，其他条件不变，（1）中的结论是否仍然成立？若成立，请直接回答；若不成立，你又能得出什么结论，直接写出你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC为等边三角形，D、E分别是AC、BC上的点，且AD=CE，AE与BD相交于点P，BF⊥AE于点F，BP=8，则PF=
-
科目： 来源： 题型：
查看答案和解析>>【题目】现有两枚质地均匀的正方体骰子，每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子，以朝上一面所标的数字为掷得的结果，那么所得结果之和为9的概率是( )
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示．A(2,3)，B(3,1)，C(-2,-2)三点在格点上．
（1）作出△ABC关于y轴对称的△A1B1C1；
（2）直接写出△ABC关于x轴对称的△A2B2C2的各点坐标；
（3）求出△ABC的周长。.
相关试题
