【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() =
=![]() .
.
(1)请直接写出AE的长是________;
(2)如图(1),若![]() 为边
为边![]() 上的点,
上的点,![]() 与
与![]() 相交于点
相交于点![]() ,且
,且![]() =
=![]() .求证:
.求证:![]() ;
;
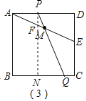
(3)如图(2),若![]() 为
为![]() 的中点,过点
的中点,过点![]() 作直线分别与
作直线分别与![]() ,
,![]() 相交于点
相交于点![]() 、
、![]() ,且
,且![]() =
=![]() .请画出示意图并求出
.请画出示意图并求出![]() 长度.
长度.

参考答案:
【答案】(1)![]() ;(2)见解析;(3)图见解析,2或3
;(2)见解析;(3)图见解析,2或3
【解析】
(1)根据正方形性质、勾股定理和含![]() 锐角的直角三角形性质即可得到结论;
锐角的直角三角形性质即可得到结论;
(2)根据正方形性质和题目条件可证明![]() ,进而可得
,进而可得![]() ;
;
(3)分两种情况画出示意图(2)和(3),在图(2)中,根据正方形性质可先证明:四边形![]() 为平行四边形,再利用勾股定理即可求得
为平行四边形,再利用勾股定理即可求得![]() ,在图(3)中,先证明
,在图(3)中,先证明![]() ,再利用勾股定理和等腰三角形性质即可求得
,再利用勾股定理和等腰三角形性质即可求得![]() .
.
解:(1)(1)![]() 四边形
四边形![]() 为正方形,
为正方形,![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
(2)如图![]() ,∵ 四边形
,∵ 四边形![]() 为正方形,
为正方形,
∴ ![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
在![]() 和
和![]() 中,
中,
![]()
∴ ![]() ,
,
∴ ![]() =
=![]() =
=![]()
∵ ![]() =
=![]()
∴ ![]() =
=![]()
∴ ![]() =
=![]()
∴ ![]() ;
;
(3)当如图(2)![]() 时,过
时,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
∵ 四边形![]() 为正方形,
为正方形,
∴ ![]() =
=![]() ,
,![]() ,
,
∴ 四边形![]() 为平行四边形,
为平行四边形,
∴ ![]() =
=![]()
∵ ![]() =
=![]()
∴ ![]() =
=![]()
由(2)可得:![]() ,
,
∴ ![]() ,
,
∴ ![]() =
=![]()
∵ ![]() 为
为![]() 的中点,
的中点,
∴ ![]() ,
,
设![]() =
=![]() ,在
,在![]() 中,
中,![]() =
=![]() ,
,
∴ ![]() =
=![]() =
=![]() ,
,
根据勾股定理得:![]() =
=![]() ,即
,即![]() ,
,
∵ ![]()
∴ ![]() =
=![]() ,
,
∴ ![]() =
=![]() =
=![]() ;
;
当如图![]() 时,过
时,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
同理可证:![]() ,
,
∴ ![]() =
=![]() =
=![]()
∴ ![]() =
=![]() =
=![]()
∴ ![]() =
=![]()
在![]() 中,
中,![]() =
=![]() ,
,
∴ ![]() =
=![]() ,
,
∴ ![]() =
=![]()
∴ ![]() ,
,![]()
根据勾股定理得:![]() =
=![]()
综上可知,![]() 的长等于
的长等于![]() 或
或![]() .
.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.
B.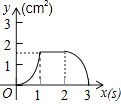
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=9,把矩形ABCD沿对角线BD折叠,使点C与点F重合,BF交AD于点M,过点C作CE⊥BF于点E,交AD于点G,则MG的长= .

-
科目: 来源: 题型:
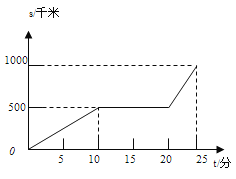
查看答案和解析>>【题目】某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中所走的路程S(米)与时间t(分)之间的关系.
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;
(2)王老师吃早餐用了多少分钟?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?吃完早餐后的平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于每个非零自然数n,抛物线y=x2﹣
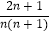 x+
x+  与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2017B2017的值是 .
与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2017B2017的值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
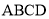 的对角线
的对角线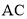 ,
,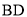 相交于点
相交于点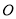 ,
,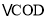 关于
关于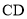 的对称图形为
的对称图形为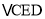 .
. (1)求证:四边形
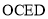 是菱形;
是菱形;(2)连接
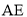 ,交
,交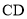 于点
于点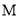 ,连接
,连接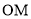 ,取
,取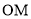 的中点
的中点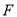 ,连接
,连接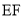 .
.①根据题意补全图形;
②若
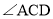 =
=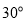 ,请用等式表示线段
,请用等式表示线段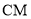 、
、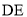 、
、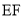 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
相关试题

