【题目】我市为全面推进“十个全覆盖”工作,绿化提质改造工程如火如荼地进行,某施工队计划购买甲、乙两种树苗共600棵对某标段道路进行绿化改造,已知甲种树苗每棵100元,乙种树苗每棵200元.
(1)若购买两种树苗的总金额为70000元,求需购买甲、乙两种树苗各多少棵?
(2)若购买甲种树苗的金额不少于购买乙种树苗的金额,至少应购买甲种树苗多少棵?
参考答案:
【答案】
(1)解:设购买甲种树苗x棵,购买乙种树苗y棵,由题意,得
![]() ,
,
解得: ![]() ,
,
答:购买甲种树苗500棵,则购买乙种树苗100棵;
(2)解:设应购买甲种树苗a棵,则购买乙种树苗(100﹣a)棵,由题意,得
100a≥200(600﹣a),
解得:a≥400.
答:至少应购买甲种树苗400棵
【解析】(1)设购买甲种树苗x棵,购买乙种树苗y棵,列出方程即可解决.(2)设应购买甲种树苗a棵,则购买乙种树苗(100﹣a)棵,列出不等式即可解决问题.本题考查了二元一次方程组的应用,一元一次不等式的解法的运用,解答时建立方程和不等式是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E、F在四边形ABCD的对角线BD所在的直线上,且BE=DF,AE∥CF,请再添加一个条件(不要在图中再增加其它线段和字母),能证明四边形ABCD是平行四边形,并证明你的想法.
你所添加的条件:____________________________________;
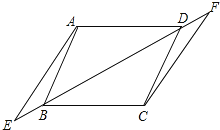
证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了8次测试,测试成绩(单位:环)如下表:
第一次
第二次
第三次
第四次
第五次
第六次
第七次
第八次
甲
10
8
9
8
10
9
10
8
乙
10
7
10
10
9
8
8
10
(1)根据表格中的数据,计算出甲的平均成绩是 9 环,乙的平均成绩是 9 环;
(2)分别计算甲、乙两名运动员8次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
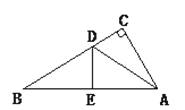
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,BC边上高AD=12,试求△ABC周长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)计算:(﹣1)2016﹣4cos60°+( )0﹣(
)0﹣(  )﹣2;
)﹣2;
(2)先化简,再求值: ,其中3x+6y﹣1=0.
,其中3x+6y﹣1=0.
相关试题

