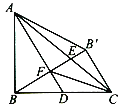
【题目】如图,点 D 是等腰直角 △ABC 腰 BC 上的中点,点B 、B′ 关于 AD 对称,且 BB′ 交AD 于 F,交 AC 于 E,连接 FC 、 AB′,下列说法:① ∠BAD=30°; ② ∠BFC=135°;③ AF=2B′ C;正确的个数是()
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】B
【解析】
依据点D是等腰直角△ABC腰BC上的中点,可得tan∠BAD=![]() ,即可得到∠BAD≠30°;连接B'D,即可得到∠BB'C=∠BB'D+∠DB'C=90°,进而得出△ABF≌△BCB',判定△FCB'是等腰直角三角形,即可得到∠CFB'=45°,即∠BFC=135°;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C;依据△AEF与△CEB'不全等,即可得到S△AFE≠S△FCE.
,即可得到∠BAD≠30°;连接B'D,即可得到∠BB'C=∠BB'D+∠DB'C=90°,进而得出△ABF≌△BCB',判定△FCB'是等腰直角三角形,即可得到∠CFB'=45°,即∠BFC=135°;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C;依据△AEF与△CEB'不全等,即可得到S△AFE≠S△FCE.
∵点D是等腰直角△ABC腰BC上的中点,
∴BD=![]() BC=
BC=![]() AB,
AB,
∴tan∠BAD=![]() ,
,
∴∠BAD≠30°,故①错误;
如图,连接B'D,
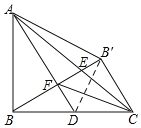
∵B、B′关于AD对称,
∴AD垂直平分BB',
∴∠AFB=90°,BD=B'D=CD,
∴∠DBB'=∠BB'D,∠DCB'=∠DB'C,
∴∠BB'C=∠BB'D+∠DB'C=90°,
∴∠AFB=∠BB'C,
又∵∠BAF+∠ABF=90°=∠CBB'+∠ABF,
∴∠BAF=∠CBB',
∴△ABF≌△BCB',
∴BF=CB'=B'F,
∴△FCB'是等腰直角三角形,
∴∠CFB'=45°,即∠BFC=135°,故②正确;
由△ABF≌△BCB',可得AF=BB'=2BF=2B'C,故③正确;
∵AF>BF=B'C,
∴△AEF与△CEB'不全等,
∴AE≠CE,
∴S△AFE≠S△FCE,故④错误;
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为 a 的正方形内去掉一个边长为 b 的小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证的等式是( )
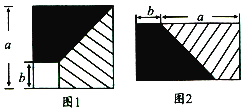
A. (a-b)2=a2-2ab+b2 B. a2+ab=a (a+b) C. (a+b)2=a2+2ab+b2 D. a2-b2=(a+b)(a-b)
-
科目: 来源: 题型:
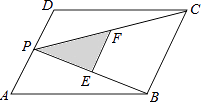
查看答案和解析>>【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1 , S2 . 若S=3,则S1+S2的值为( )
A.24
B.12
C.6
D.3 -
科目: 来源: 题型:
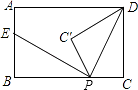
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华通过学习函数发现:若二次函数y=ax2+bx+c(a≠0)的图象经过点(x1 , y1),(x2 , y2)(x1<x2),若y1y2<0,则方程ax2+bx+c=0(a≠0)的一个根x0的取值范围是x1<x0<x2 , 请你类比此方法,推断方程x3+x﹣1=0的实数根x0所在范围为( )
A.﹣ <x0<0
<x0<0
B.0<x0<
C. <x0<1
<x0<1
D.1<x0<
-
科目: 来源: 题型:
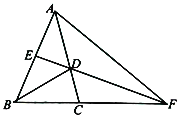
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD是∠B的平分线,交AC于点D,E是AB中点,ED交BC的延长线于点F.求证:AB=CF.
相关试题

