【题目】完成下列证明:
如图,已知DE⊥AC于点E,BC⊥AC于点C,FG⊥AB于点G,∠1=∠2,求证:CD⊥AB.
证明:∵DE⊥AC,BC⊥AC(已知),
∴DE∥(),
∴∠2=(两直线平行,内错角相等),
∵∠1=∠2,(已知),
∴∠1=(),
∴GF∥CD(),
∵FG⊥AB(已知),
∴CD⊥AB.
参考答案:
【答案】BC;在同一平面内,垂直于同一直线的两直线平行;∠BCD;∠BCD;等量代换;同位角相等,两直线平行
【解析】证明:∵DE⊥AC,BC⊥AC(已知),
∴DE∥BC( 在同一平面内,垂直于同一直线的两直线平行),
∴∠2=∠BCD(两直线平行,内错角相等),
∵∠1=∠2,(已知),
∴∠1=∠BCD(等量代换),
∴GF∥CD(同位角相等,两直线平行),
∵FG⊥AB(已知),
∴CD⊥AB,
所以答案是:1.BC;2在同一平面内,垂直于同一直线的两直线平行;3.∠BCD;4.∠BCD;5.等量代换;6.同位角相等,两直线平行.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在
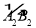 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AB是⊙O的直径,E是AB延长线上一点,EC切⊙O于点C,OP⊥AO交AC于点P,交EC的延长线于点D.
(1)求证:△PCD是等腰三角形;
(2)CG⊥AB于H点,交⊙O于G点,过B点作BF∥EC,交⊙O于点F,交CG于Q点,连接AF,如图2,若sinE=
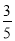 ,CQ=5,求AF的值.
,CQ=5,求AF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠AGE,∠D=∠1,且∠1+∠2=180°,则下列结论:①CE∥BF,②∠A=∠D,③AB∥CD,④∠C=∠B,其中正确的结论有( )
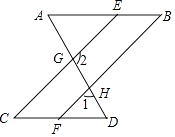
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点P(3a,a)是反比例函数y=
 (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
A.y=
B.y=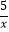
C.y=
D.y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值: (
 a2bab2)(1
a2bab2)(1 ab2a2b) ,其中 a=3, b=2 .
ab2a2b) ,其中 a=3, b=2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把点P(-1,-2)向上平移4个单位长度所得点的坐标是___________.
相关试题

