【题目】如图,在数轴上点A表示数20,点C表示数30,我们把数轴上两点之间的距离用表示两点的大写字母一起标记.
比如,点A与点B之间的距离记作AB,点B与点C之间的距离记作BC…
![]()
(1)点A与点C之间的距离记作AC,则AC的长为________;若数轴上有一点D满足CD=AD,则D点表示的数为___________;
(2)动点B从数1对应的点开始向右运动,速度为每秒1个单位长度,同时点A、C在数轴上运动,点A、C的速度分别为每秒2个单位长度,每秒3个单位长度,运动时间为t秒.
①若点A向右运动,点C向左运动,AB=BC,求t的值;
②若点A向左运动,点C向右运动,2ABm×BC的值不随时间t的变化而改变,则2ABm×BC的值为_____________(直接写出答案).
参考答案:
【答案】(1)50;5; (2)①t=10或![]() ;②-45.
;②-45.
【解析】
(1)在数轴上表示两点所组成的线段长度用右边点所表示的数减去左边点所表示的数即可.
(2)当数轴上想表示两个点之间的距离,根据绝对值的意义可用绝对值进行处理.动点在数轴上运动,在已知运动的方向和速度之后,就可以利用原来所在的数如果向右移动就加上向右移动的距离,如果向左移动,就减去向左移动的距离.
解:(1)∵A表示的数为-20,C表示的数为30,
∴AC=30-(-20)=50;
∵CD=AD
∴点D为AC的中点
∴D所表示的数为![]()
![]() =5,
=5,
故答案为50;5
(2)①根据题意,A所表示的数为-20+2t,C所表示的数为30-3t,B所表示的数为1+t,
AB=|-20+2t-(1+t)|=|-21+t|,
BC=|30-3t-(1+t)|=|29-4t|,
∵AB=BC
∴|-21+t|=|29-4t|,
-21+t=29-4t,
解得t=10,
-21+t=4t-29
解得t=![]() .
.
∴当AB=BC时,t=10或![]() .
.
②根据题意,A所表示的数为-20-2t,B所表示的数为1+t,C所表示的数为30+3t,
AB=1+t-(-20-2t)=21+3t,
BC=30+3t-(1+t)=29+2t,
∴2AB-m×BC=2(21+3t)-m×(29+2t)=42+6t-29m-2mt,
∵2AB-m×BC的值不随时间t的变化而改变,
∴6t-2mt=0,
∴m=3,
∴42+6t-29m-2mt=-45,
∴2AB-m×BC=-45.
故答案为-45.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若一个关于x的方程
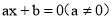 的解为
的解为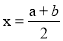 ,则称此方程为“中点方程”.如:
,则称此方程为“中点方程”.如: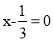 的解为
的解为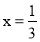 ,而
,而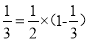 ;
;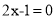 的解为
的解为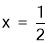 ,而
,而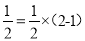 .
.(1)若
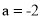 ,有符合要求的“中点方程”吗?若有,请求出该方程的解;若没有请说明理由;
,有符合要求的“中点方程”吗?若有,请求出该方程的解;若没有请说明理由;(2)若关于x的方程
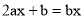 是“中点方程”,求代数式
是“中点方程”,求代数式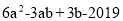 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】把所有正偶数从小到大排列,并按如下规律分组:
第一组:2,4;
第二组:6,8,10,12;
第三组:14,16,18,20,22,24
第四组:26,28,30,32,34,36,38,40
……
则现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到右数),如A10=(2,3),则A2018=( )
A. (31,63) B. (32,17) C. (33,16) D. (34,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了奖励优秀班集体,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元,购买3幅乒乓球拍和2幅羽毛球拍共需204元.
(1)每副乒乓球拍和羽毛球拍的单价各是多少元?
(2)若学校购买5副乒乓球拍和3副羽毛球拍,一共应支出多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我区实施课堂教学改革后,学生的自主学习、合作交流能力有很大提高,为了解学生自主学习、合作交流的具体情况,张老师对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
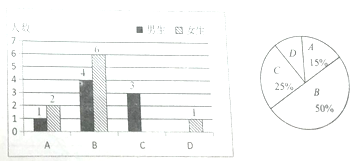
(1)本次调查中,张老师一共调查了_____名同学;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列货车从北京开往乌鲁木齐,以58km/h的平均速度行驶需要65h.为了实施西部大开发,京乌线决定全线提速.
(1)如果提速后平均速度为vkm/h,全程运营时间为t小时,试写出t与v之间的函数表达式;
(2)如果提速后平均速度为78km/h,求提速后全程运营时间;
(3)如果全程运营的时间控制在40h内,那么提速后,平均速度至少应为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=DC,E,F,G,H分别是AD,BC,BD,AC的中点.
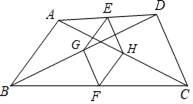
(1)证明:EG=EH;(2)证明:四边形EHFG是菱形.
相关试题

