[题目]解下列方程和不等式:(1)(3x)2(2x+1)(3x2) = 3(x+2)2(2)(3x+2)2(9x4)x+4=0(3)(13x)2+(2x1)2>13(x1)(x+1)(4)(2x1)2(13x)2＜5(1x)(x+1) 题目和参考答案 ——青夏教育精英家教网—

【题目】解下列方程和不等式：

(1)(3x)2(2x+1)(3x2) = 3(x+2)2

(2)(3x+2)2(9x4)x+4=0

(3)(13x)2+(2x1)2>13(x1)(x+1)

(4)(2x1)2(13x)2＜5(1x)(x+1)

参考答案：

【答案】（1）；（2）x=0.5；（3）；（4）x＜2.5.

【解析】试题分析：（1）（2）根据整式混合运算法则化简，解方程即可；

（3）（4）根据整式混合运算法则化简，解不等式即可．

试题解析：解：（1） 9x2-（6x2-x-2）=3（x2+4x+4）

9x2-6x2+x+2=3x2+12x+12

-11x=10

（2） 9x2+12x+4-（9x2-4x）+4=0

9x2+12x+4-9x2+4x+4=0

16x+8=0

x=0.5

（3）16x+9x2+4x24x+1＞13x213，

210x＞-13，

∴x＜

（4）4x2-4x+1-（1-6x+9x2）＜5（1-x2）

4x2-4x+1-1+6x-9x2＜5-5x2

2x＜5

∴x＜2.5

相关试题

科目： 来源： 题型：

【题目】用一个平面去截一个圆锥，截面的形状不可能是( )
A.圆B.矩形C.椭圆D.三角形
查看答案和解析>>
科目： 来源： 题型：

【题目】（1）从四边形的一个顶点出发可以画_____条对角线，把四边形分成了个三角形；四边形共有____条对角线．
（2）从五边形的一个顶点出发可以画_____条对角线，把五边形分成了个三角形；五边形共有____条对角线．
（3）从六边形的一个顶点出发可以画_____条对角线，把六边形分成了个三角形；六边形共有____条对角线．
（4）猜想：①从100边形的一个顶点出发可以画_____条对角线，把100边形分成了个三角形；100边形共有___条对角线．②从n边形的一个顶点出发可以画_____条对角线，把n分成了个三角形；n边形共有_____条对角线．
查看答案和解析>>
科目： 来源： 题型：

【题目】计算题
（1）计算：| ﹣2|+（）﹣1﹣（π﹣3.14）0﹣ ；
（2）计算：[xy（3x﹣2）﹣y（x2﹣2x）]÷x2y．
查看答案和解析>>
科目： 来源： 题型：

【题目】若在方格（每小格正方形边长为1m）上沿着网格线平移，规定：沿水平方向平移的数量为a（向右为正，向左为负，平移|a|个单位），沿竖直方向平移的数量为b（向上为正，向下为负，平移|b|个单位），则把有序数对{a，b}叫做这一平移的“平移量”．例如：点A按“平移量”{1，4}可平移至点B．
（1）从点C按“平移量”{ ， }可平移到点B；
（2）若点B依次按“平移量”{4，﹣3}、{﹣2，1}平移至点D， ①请在图中标出点D；（用黑色水笔在答题卡上作出点D）
②如果每平移1m需要2.5秒，那么按此方法从点B移动至点D需要多少秒？
③观察点D的位置，其实点B也可按“平移量”{ ， }直接平移至点D；观察这两种平移的“平移量”，猜想：点E依次按“平移量”{2a，3b}、{﹣5a，b}、{a，﹣5b}平移至点F，则相当于点E按“平移量”{ ， }直接平移至点F．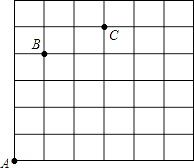
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在平面直角坐标系xOy中，顶点为M的抛物线y=ax2+bx（a＞0），经过点A和x轴正半轴上的点B，AO=OB=2，∠AOB=120°．
（1）求这条抛物线的表达式；
（2）连接OM，求∠AOM的大小；
（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．
查看答案和解析>>
科目： 来源： 题型：

【题目】观察1+3=4=22 1+3+5=9=32 1+3+5+7=16=42 1+3+5+7+9=25=52 ……
(1)根据以上规律，猜测1+3+5+7+…+(2n1)=__________；
(2)用文字语言叙述你所发现的规律.
查看答案和解析>>