【题目】如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0),经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=120°.
(1)求这条抛物线的表达式;
(2)连接OM,求∠AOM的大小;
(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.

参考答案:
【答案】(1) y=![]() x2﹣
x2﹣![]() x;(2) ∠AOM=150°;(3)点C的坐标为:(4,0)或(8,0).
x;(2) ∠AOM=150°;(3)点C的坐标为:(4,0)或(8,0).
【解析】
试题分析:(1)根据AO=OB=2,∠AOB=120°,求出A点坐标,以及B点坐标,进而利用待定系数法求二次函数解析式;(2)根据(1)中解析式求出M点坐标,再利用锐角三角函数关系求出∠FOM=30°,进而得出答案;(3)分别根据当△ABC1∽△AOM以及当△C2BA∽△AOM时,利用相似三角形的性质求出C点坐标即可.
试题解析:(1)过点A作AE⊥y轴于点E,
∵AO=OB=2,∠AOB=120°,
∴∠AOE=30°,
∴OE=![]() ,AE=1,
,AE=1,
∴A点坐标为:(﹣1,![]() ),B点坐标为:(2,0),
),B点坐标为:(2,0),
将两点代入y=ax2+bx得:
 ,
,
解得: ,
,
∴抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x;
x;

(2)过点M作MF⊥OB于点F,
∵y=![]() x2﹣
x2﹣![]() x=
x=![]() (x2﹣2x)=
(x2﹣2x)=![]() (x2﹣2x+1﹣1)=
(x2﹣2x+1﹣1)=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() ,
,
∴M点坐标为:(1,﹣![]() ),
),
∴tan∠FOM=![]() =
=![]() ,
,
∴∠FOM=30°,
∴∠AOM=30°+120°=150°;
(3)当点C在x轴负半轴上时,则∠BAC=150°,而∠ABC=30°,此时∠C=0°,故此种情况不存在;
当点C在x轴正半轴上时,
∵AO=OB=2,∠AOB=120°,
∴∠ABO=∠OAB=30°,
∴AB=2EO=2![]() ,
,
当△ABC1∽△AOM,
∴![]() ,
,
∵MO=![]() =
=![]() ,
,
∴ ,
,
解得:BC1=2,∴OC1=4,
∴C1的坐标为:(4,0);
当△C2BA∽△AOM,
∴![]() ,
,
∴ ,
,
解得:BC2=6,∴OC2=8,
∴C2的坐标为:(8,0).
综上所述,△ABC与△AOM相似时,点C的坐标为:(4,0)或(8,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:| ﹣2|+(
﹣2|+(  )﹣1﹣(π﹣3.14)0﹣
)﹣1﹣(π﹣3.14)0﹣  ;
;
(2)计算:[xy(3x﹣2)﹣y(x2﹣2x)]÷x2y. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程和不等式:
(1)(3x)2(2x+1)(3x2) = 3(x+2)2
(2)(3x+2)2(9x4)x+4=0
(3)(13x)2+(2x1)2>13(x1)(x+1)
(4)(2x1)2(13x)2<5(1x)(x+1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若在方格(每小格正方形边长为1m)上沿着网格线平移,规定:沿水平方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿竖直方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”.例如:点A按“平移量”{1,4}可平移至点B.
(1)从点C按“平移量”{ , }可平移到点B;
(2)若点B依次按“平移量”{4,﹣3}、{﹣2,1}平移至点D, ①请在图中标出点D;(用黑色水笔在答题卡上作出点D)
②如果每平移1m需要2.5秒,那么按此方法从点B移动至点D需要多少秒?
③观察点D的位置,其实点B也可按“平移量”{ , }直接平移至点D;观察这两种平移的“平移量”,猜想:点E依次按“平移量”{2a,3b}、{﹣5a,b}、{a,﹣5b}平移至点F,则相当于点E按“平移量”{ , }直接平移至点F.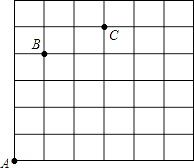
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察1+3=4=22 1+3+5=9=32 1+3+5+7=16=42 1+3+5+7+9=25=52 ……
(1)根据以上规律,猜测1+3+5+7+…+(2n1)=__________;
(2)用文字语言叙述你所发现的规律.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种细胞的直径0.000 000 95米,将0.000 000 95用科学计数法表示为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(1,-2)关于y轴对称的点的坐标是( )
A. (1,2) B. (-1,2) C. (-1,-2) D. (-2,1)
相关试题

