【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=﹣1是对称轴,有下列判断:
①b﹣2a=0;②4a﹣2b+c<0;③a﹣b+c=﹣9a;④若(﹣3,y1),( ![]() ,y2)是抛物线上两点,则y1>y2 , 其中正确的是( )
,y2)是抛物线上两点,则y1>y2 , 其中正确的是( )
A.①②③
B.①③④
C.①②④
D.②③④
参考答案:
【答案】B
【解析】解:∵抛物线的对称轴是直线x=﹣1,
∴﹣ ![]() =﹣1,
=﹣1,
b=2a,
∴b﹣2a=0,
故①正确;
∵抛物线的对称轴是直线x=﹣1,和x轴的一个交点是(2,0),
∴抛物线和x轴的另一个交点是(﹣4,0),
∴把x=﹣2代入得:y=4a﹣2b+c>0,
故②错误;
∵图象过点(2,0),代入抛物线的解析式得:4a+2b+c=0,
又∵b=2a,
∴c=﹣4a﹣2b=﹣8a,
∴a﹣b+c=a﹣2a﹣8a=﹣9a,
故③正确;
根据图象,可知抛物线对称轴的右边y随x的增大而减小,
∵抛物线和x轴的交点坐标是(2,0)和(﹣4,0),抛物线的对称轴是直线x=﹣1,
∴点(﹣3,y1)关于对称轴的对称点的坐标是((1,y1),
∵( ![]() ,y2),1<
,y2),1< ![]() ,
,
∴y1>y2,
故④正确;
即正确的有①③④,
所以答案是:B.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形
 中,
中, ,
, ,点
,点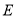 是
是 的中点,动点
的中点,动点 从
从 点出发,以每秒
点出发,以每秒 的速度沿
的速度沿 运动,最终到达点
运动,最终到达点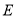 .若点
.若点 运动的时间为
运动的时间为 秒,那么当
秒,那么当 _____________秒时,
_____________秒时, 的面积等于
的面积等于 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于点E,则sin∠E的值是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在图中利用网格点和三角板画图或计算:
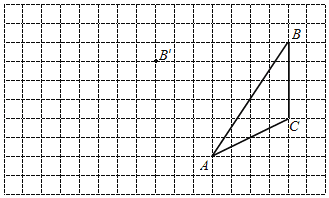
(1)在给定方格纸中画出
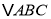 平移后的
平移后的 (点
(点 的对应点是点
的对应点是点 );
);(2)画出
 边上的中线
边上的中线 ;
;(3)画出
 边上的高线
边上的高线 ;
;(4)记网格的边长为1,则在平移的过程中线段
 扫过区域的面积为
扫过区域的面积为 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是边BC上一点,DE⊥AB,DF⊥AC,垂足分别是E,F,△AEF∽△ABC.

(1)求证:△AED≌△AFD;
(2)若BC=2AD,求证:四边形AEDF是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB

(1)求证:DE与⊙O相切;
(2)若∠C=30°,求∠BOD的度数;
(3)在(2)的条件下,若⊙O半径为2,求阴影部分面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b(a≠0)的图形与反比例函数y=
 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=  ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2).
(1)求该反比例函数和一次函数的解析式.
(2)求△AOC的面积.
相关试题

