Question

【题目】如图，一次函数y=ax+b（a≠0）的图形与反比例函数y= （k≠0）的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=3，tan∠AOH= ，点B的坐标为（m，﹣2）．

（1）求该反比例函数和一次函数的解析式．
（2）求△AOC的面积．

Answer 1

【答案】
（1）解：∵OH=3，tan∠AOH= ，

∴AH=OHtan∠AOH=4，

∴点A的坐标为（﹣4，3）．

∵点A在反比例函数y= （k≠0）的图象上，

∴k=﹣4×3=﹣12，

∴反比例函数解析式为y=﹣ ．

∵点B（m，﹣2）在反比例函数y=﹣ 的图象上，

∴m=﹣ =6，

∴点B的坐标为（6，﹣2）．

将A（﹣4，3）、B（6，﹣2）代入y=ax+b，

，解得： ，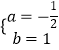

∴一次函数的解析式为y=﹣ x+1

（2）解：当x=0时，y=﹣ x+1=1，

∴点C的坐标为（0，1），

∴OC=1，

∴S△AOC= OCAH= ×1×4=2．

【解析】（1）由OH=3，tan∠AOH即可求出点A的坐标，利用反比例函数上点的坐标特点即可求出K值及点B的坐标，再根据A、B的坐标利用待定系数法即可求出直线直线AB的解析式；（2）将X=0代入直线AB的解析式，中求出Y的值，由此可得出OC的长，再根据三角形的面积公式即可求出△AOC的面积。