搜索
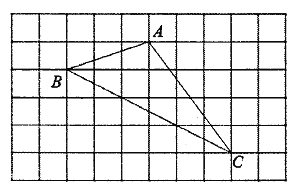
【题目】如图，已知所有小正方形的边长都为1，点
、
、
都在格点上，借助网格完成下列各题.
（1）过点画直线
的垂线，并标出垂足
;
（2）线段______的长度是点到直线
的距离；
（3）过点画直线
的平行线交于格点
，求出四边形
的面积.
参考答案：
【答案】(1)画图见解析；（2）线段CD的长度是点
到直线
的距离；（3）四边形
的面积为：15
【解析】
(1)利用格线画AD⊥BC于点D;
（2）利用点到直线的距离进行解答即可；
（3）画
方格的对角线得到CE//AB,利用平行四边形特征求出四边形的面积
(1)∵如图：
又∵
∴
∴
∴AD⊥BC
∴如图所示：AD为所求；
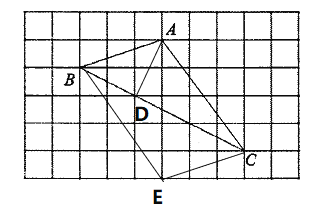
（2）线段CD的长度是点到直线的距离；
（3）如图所示：E为所求；CE//AB,连接BE
∵
∵
∴
∴四边形是平行四边形
∴
∴四边形的面积为：15
-
科目： 来源： 题型：
查看答案和解析>>【题目】哈市某专卖店销售某品牌服装，设服装进价为80元，当每件服装售价为240元时，月销售为200件，该专卖店为提高经营利润，准备采取降价的方式进行促销，经市场调查发现：当每件价格每下降10元时，月销售量就会增加20件，设每件服装售价为x(元)，该专卖店的月利润为y(元).
(1)求出y与x的函数关系式(不要求写出x的取值范围)；
(2)该专卖店要获得最大月利润，售价应定为每件多少元？最大利润是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知反比例函数y＝
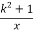的图上象有三个点（2，y1），（3，y2），（﹣1，y3），则y1，y2，y3的大小关系是（ ）A. y1＞y2＞y3B. y2＞y1＞y3C. y3＞y1＞y2D. y3＞y2＞y1
-
科目： 来源： 题型：
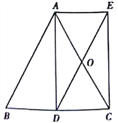
查看答案和解析>>【题目】如图，AD是等腰△ABC底边BC上的高，点O是AC中点，延长DO到E
使AE∥BC，连接AE。
（1）求证：四边形ADCE是矩形；
（2）①若AB=17，BC=16，则四边形ADCE的面积＝ ；
②若AB=10，则BC＝ 时，四边形ADCE是正方形。
-
科目： 来源： 题型：
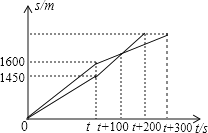
查看答案和解析>>【题目】在一次越野赛跑中，当小明跑了1600m时，小刚跑了1450m，此后两人分别调整速度，并以各自新的速度匀速跑，又过100s时小刚追上小明，200s时小刚到达终点，300s时小明到达终点．他们赛跑使用时间t（s）及所跑距离如图s（m），这次越野赛的赛跑全程为 m？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,直线y=kx+k交x轴,y轴分别于A,C,直线BC过点C交x轴于B,OC=3OA,∠CBA=45.
(1)求直线BC的解析式；
(2)动点P从A出发沿射线AB匀速运动，速度为2个单位/秒，连接CP，设△PBC的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式，直接写出t的取值范围；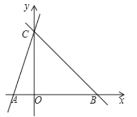
-
科目： 来源： 题型：
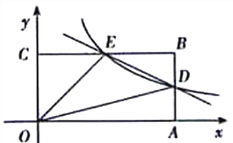
查看答案和解析>>【题目】如图，在平面直角坐标系中，原点O是矩形OABC的一个顶点，点A、C都
在坐标轴上，点B的坐标是(4.2)，反比例函数
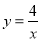与AB，BC分别交于点D，E。(1)求直线DE的解析式；
(2)若点F为y轴上一点，△OEF和△ODE的面积相等，求点F的坐标。
相关试题
