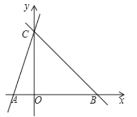
【题目】如图,直线y=kx+k交x轴,y轴分别于A,C,直线BC过点C交x轴于B,OC=3OA,∠CBA=45.
(1)求直线BC的解析式;
(2)动点P从A出发沿射线AB匀速运动,速度为2个单位/秒,连接CP,设△PBC的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式,直接写出t的取值范围;
参考答案:
【答案】(1) BC的解析式是y=x+3;(2)当0<t2时, S=3t+6;当t>2时,S=3t6.
【解析】
(1)令y=0,即可求得A的坐标,根据OC=3OA即可求得C的坐标,再根据∠CBA=45°,即△BOC的等腰直角三角形,则B的坐标即可求得,然后利用待定系数法求得BC的解析式;
(2)分成P在AB和在AB的延长线上两种情况进行讨论,利用三角形面积公式即可求解.
(1)在y=kx+k中,令y=0,则x=1,即A的坐标是(1,0).
∵OC=3OA,
∴OC=3,即C的坐标是(0,3).
∵∠CBA=45,
∴∠OCB=∠CBA=45,
∴OB=OC=3,则B的坐标是(3,0).
设BC的解析式是y=kx+b,则![]() ,
,
解得:![]() ,
,
则BC的解析式是y=x+3;
(2)当0<t2时,P在线段AB上,则BP=42t,
则S=![]() (42t)×3=3t+6;
(42t)×3=3t+6;
当t>2时,OP=2t4,则S=![]() ×3(2t4),即S=3t6.
×3(2t4),即S=3t6.
-
科目: 来源: 题型:
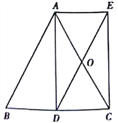
查看答案和解析>>【题目】如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E
使AE∥BC,连接AE。
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积= ;
②若AB=10,则BC= 时,四边形ADCE是正方形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知所有小正方形的边长都为1,点
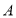 、
、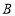 、
、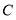 都在格点上,借助网格完成下列各题.
都在格点上,借助网格完成下列各题.(1)过点
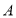 画直线
画直线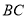 的垂线,并标出垂足
的垂线,并标出垂足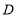 ;
;(2)线段______的长度是点
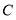 到直线
到直线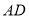 的距离;
的距离;(3)过点
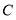 画直线
画直线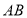 的平行线交于格点
的平行线交于格点 ,求出四边形
,求出四边形 的面积.
的面积.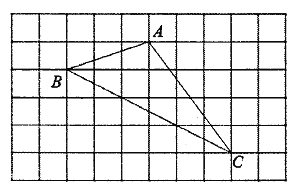
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次越野赛跑中,当小明跑了1600m时,小刚跑了1450m,此后两人分别调整速度,并以各自新的速度匀速跑,又过100s时小刚追上小明,200s时小刚到达终点,300s时小明到达终点.他们赛跑使用时间t(s)及所跑距离如图s(m),这次越野赛的赛跑全程为 m?
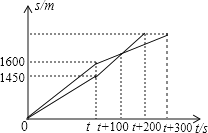
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,原点O是矩形OABC的一个顶点,点A、C都
在坐标轴上,点B的坐标是(4.2),反比例函数
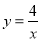 与AB,BC分别交于点D,E。
与AB,BC分别交于点D,E。(1)求直线DE的解析式;
(2)若点F为y轴上一点,△OEF和△ODE的面积相等,求点F的坐标。
-
科目: 来源: 题型:
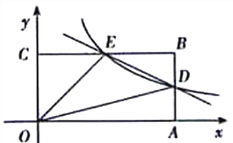
查看答案和解析>>【题目】已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.
求:(1)坡顶A到地面PO的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
-
科目: 来源: 题型:
查看答案和解析>>【题目】州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)

请根据图中提供的信息,回答下列问题:
(1)a= ,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该县共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
相关试题

