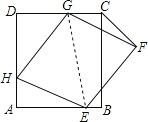
【题目】如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.

参考答案:
【答案】详见解析
【解析】
试题分析:(1)连接GE,根据正方形的性质和平行线的性质得到∠AEG=∠CGE,根据菱形的性质和平行线的性质得到∠HEG=∠FGE,解答即可;
(2)证明Rt△HAE≌Rt△GDH,得到∠AHE=∠DGH,证明∠GHE=90°,根据正方形的判定定理证明.
证明:(1)连接GE,
∵AB∥CD,
∴∠AEG=∠CGE,
∵GF∥HE,
∴∠HEG=∠FGE,
∴∠HEA=∠CGF;
(2)∵四边形ABCD是正方形,
∴∠D=∠A=90°,
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△HAE和Rt△GDH中,
![]() ,
,
∴Rt△HAE≌Rt△GDH(HL),
∴∠AHE=∠DGH,又∠DHG+∠DGH=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴菱形EFGH为正方形;
-
科目: 来源: 题型:
查看答案和解析>>【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做等邻边四边形.
(1)如图1,四边形ABCD中,AC平分∠BAD,∠B=∠D.求证:四边形ABCD为等邻边四边形.
(2)如图2,Rt△ABC中,∠ABC=90°,AB=2,BC=1,将△ABC沿∠ABC的平分线BB′的方向平移,得到△A′B′C′,连接AA′、BC′,若平移后的四边形ABC′A′是等邻边四边形,且满足BC′=AB,求平移的距离.
(3)如图3,在等邻边四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC和BD为四边形对角线,△BCD为等边三角形,试探究AC和AB的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数
1
2
3
4
5
小王
60
75
100
90
75
小李
70
90
100
80
80
根据上表解答下列问题:
(1)完成下表:
姓名
平均成绩(分)
中位数(分)
众数(分)
方差
小王
80
75
75
190
小李
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).

-
科目: 来源: 题型:
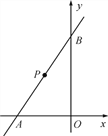
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A,B两点,且△ABO的面积为12.
(1)求k的值;
(2)若点P为直线AB上的一动点,P点运动到什么位置时,△PAO是以OA为底的等腰三角形?求出此时点P的坐标;
(3)在(2)的条件下,连接PO,△PBO是等腰三角形吗?如果是,试说明理由;如果不是,请在线段AB上求一点C,使得△CBO是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果多项式16x2+1加上一个单项式后成为一个多项式的完全平方,则这个单项式是____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.
(1)求抛物线的解析式;
(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值?如果是,请求出此定值;如果不是,请说明理由;
(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.

相关试题

