【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数![]() (x>0)图象上的点在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)4;(2)存在,P点坐标为(![]() ,0).
,0).
【解析】试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.
试题解析:(1)由y=2x+2可知A(0,2),即OA=2.
∵tan∠AHO=2,∴OH=1.
∵MH⊥x轴,∴点M的横坐标为1.
∵点M在直线y=2x+2上,
∴点M的纵坐标为4.即M(1,4).
∵点M在y=![]() 上,
上,
∴k=1×4=4.
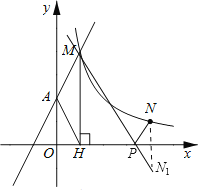
(2)存在.
过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示).此时PM+PN最小.
∵点N(a,1)在反比例函数y=![]() (x>0)上,
(x>0)上,
∴a=4.即点N的坐标为(4,1).
∵N与N1关于x轴的对称,N点坐标为(4,1),
∴N1的坐标为(4,-1).
设直线MN1的解析式为y=kx+b.
由![]()
解得k=-![]() ,b=
,b=![]() .
.
∴直线MN1的解析式为y=![]() x+
x+![]() .
.
令y=0,得x=![]() .
.
∴P点坐标为(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB =90°,∠ABC=30°,将△ABC绕点C顺时针旋转
 角(0°<
角(0°<  <180°)至△A′B′C , 使得点A′恰好落在AB边上,则
<180°)至△A′B′C , 使得点A′恰好落在AB边上,则  等于( ).
等于( ).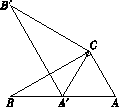
A.150°
B.90°
C.60°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点
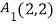 在直线
在直线  上,过点
上,过点 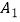 作
作 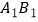 ∥y轴,交直线
∥y轴,交直线 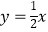 于点
于点 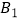 ,以
,以 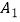 为直角顶点,
为直角顶点, 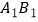 为直角边,在
为直角边,在 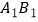 的右侧作等腰直角三角形
的右侧作等腰直角三角形  ;再过点
;再过点 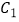 作
作 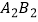 ∥y轴,分别交直线
∥y轴,分别交直线  和
和 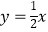 于
于 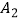 ,
, 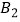 两点,以
两点,以 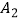 为直角顶点,
为直角顶点, 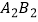 为直角边,在
为直角边,在 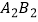 的右侧作等腰直角三角形
的右侧作等腰直角三角形  ,…,按此规律进行下去,点
,…,按此规律进行下去,点  的横坐标为 , 点
的横坐标为 , 点  的横坐标为 , 点
的横坐标为 , 点  的横坐标为 . (用含n的式子表示,n为正整数)
的横坐标为 . (用含n的式子表示,n为正整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2+6x﹣3=0,原方程可变形为( )
A.(x+3)2=9B.(x+3)2=12C.(x+3)2=15D.(x+3)2=39
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学实践探究活动中,大家遇到了这样的问题:
如图,在一个圆柱体形状的包装盒的底部A处有一只壁虎,在顶部B处有一只小昆虫,壁虎沿着什么路线爬行,才能以最短的路线接近小昆虫?
楠楠同学设计的方案是壁虎沿着A﹣C﹣B爬行;
浩浩同学设计的方案是将包装盒展开,在侧面展开图上连接AB,然后壁虎在包装盒的表面上沿着AB爬行.
在这两位同学的设计中,哪位同学的设计是最短路线呢?他们的理论依据是什么?( )
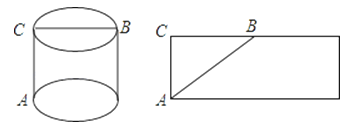
A. 楠楠同学正确,他的理论依据是“直线段最短”
B. 浩浩同学正确,他的理论依据是“两点确定一条直线”
C. 楠楠同学正确,他的理论依据是“垂线段最短”
D. 浩浩同学正确,他的理论依据是“两点之间,线段最短”
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4
 a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长.
相关试题

