【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).
(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.
参考答案:
【答案】
(1)解:∵令﹣x2+2x+3=0,解得:x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0).
设抛物线l2的解析式为y=a(x+1)(x﹣4).
∵将D(0,﹣2)代入得:﹣4a=﹣2,
∴a= ![]() .
.
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣2
x﹣2
(2)解:①如图1所示:
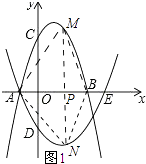
∵A(﹣1,0),B(3,0),
∴AB=4.
设P(x,0),则M(x,﹣x2+2x+3),N(x, ![]() x2﹣
x2﹣ ![]() x﹣2).
x﹣2).
∵MN⊥AB,
∴SAMBN= ![]() ABMN=﹣3x2+7x+10(﹣1<x<3).
ABMN=﹣3x2+7x+10(﹣1<x<3).
∴当x= ![]() 时,SAMBN有最大值.
时,SAMBN有最大值.
∴此时P的坐标为( ![]() ,0).
,0).
②如图2所示:作CG⊥MN于G,DH⊥MN于H,如果CM与DN不平行.
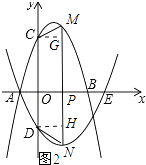
∵DC∥MN,CM=DN,
∴四边形CDNM为等腰梯形.
∴∠DNH=∠CMG.
在△CGM和△DNH中 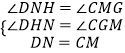 ,
,
∴△CGM≌△DNH.
∴MG=HN.
∴PM﹣PN=1.
设P(x,0),则M(x,﹣x2+2x+3),N(x, ![]() x2﹣
x2﹣ ![]() x﹣2).
x﹣2).
∴(﹣x2+2x+3)+( ![]() x2﹣
x2﹣ ![]() x﹣2)=1,解得:x1=0(舍去),x2=1.
x﹣2)=1,解得:x1=0(舍去),x2=1.
∴P(1,0).
当CM∥DN时,如图3所示:
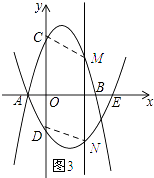
∵DC∥MN,CM∥DN,
∴四边形CDNM为平行四边形.
∴DC=MN=5
∴﹣x2+2x+3﹣( ![]() x2﹣
x2﹣ ![]() x﹣2)=5,
x﹣2)=5,
∴x1=0(舍去),x2= ![]() ,
,
∴P( ![]() ,0).
,0).
总上所述P点坐标为(1,0),或( ![]() ,0)
,0)
【解析】根据二次函数y=﹣x2+2x+3与x轴交于点A、B(点A在点B左边),得到﹣x2+2x+3=0,求出A(﹣1,0),B(3,0),根据抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2),得到抛物线的解析式;(2)①由AB=4,MN⊥AB,得到SAMBN=![]() ABMN,此时P的坐标为(
ABMN,此时P的坐标为( ![]() ,0);②如图2所示,如果CM与DN不平行,由DC∥MN,CM=DN,得到四边形CDNM为等腰梯形,△CGM≌△DNH,PM﹣PN=1,得到P(1,0);当CM∥DN时,如图3所示,得到四边形CDNM为平行四边形,DC=MN=5,得到P(
,0);②如图2所示,如果CM与DN不平行,由DC∥MN,CM=DN,得到四边形CDNM为等腰梯形,△CGM≌△DNH,PM﹣PN=1,得到P(1,0);当CM∥DN时,如图3所示,得到四边形CDNM为平行四边形,DC=MN=5,得到P(![]() ,0);总上所述P点坐标为(1,0),或(
,0);总上所述P点坐标为(1,0),或(![]() ,0);此题是综合题,难度较大,计算和解方程时需认真仔细.
,0);此题是综合题,难度较大,计算和解方程时需认真仔细.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个正方形纸片OABC放置在平面直角坐标系中,其中A(1,0),C(0,1),P为AB边上一个动点,折叠该纸片,使O点与P点重合,折痕l与OP交于点M,与 对角线AC交于Q点
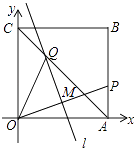
(Ⅰ)若点P的坐标为(1, ),求点M的坐标;
),求点M的坐标;
(Ⅱ)若点P的坐标为(1,t)
①求点M的坐标(用含t的式子表示)(直接写出答案)
②求点Q的坐标(用含t的式子表示)(直接写出答案)
(Ⅲ)当点P在边AB上移动时,∠QOP的度数是否发生变化?如果你认为不发生变化,写出它的角度的大小.并说明理由;如果你认为发生变化,也说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】图1中的长方形长为宽的3倍,将四个这样的长方形拼成图2中的大正方形.
(1)若中间小正方形的面积是
 ,问图1中的长方形的面积是多少
,问图1中的长方形的面积是多少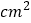 ?
? (2)若大正方形的面积就比小正方形的面积大
 ,求中间小正方形的面积.
,求中间小正方形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1为深50cm的圆柱形容器,底部放入一个长方体的铁块,现在以一定的速度向容器内注水,图2为容器顶部离水面的距离y(cm)随时间t(分钟)的变化图象,则( )
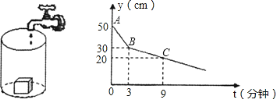
A. 注水的速度为每分钟注入
 cm高水位的水
cm高水位的水B. 放人的长方体的高度为30cm
C. 该容器注满水所用的时间为21分钟
D. 此长方体的体积为此容器的体积的0.35.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器超出5个的部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x(x>5)个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)当需要购买50个计算器时,买哪种品牌的计算器更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来根据以上信息,解答下列问题:
(1)设租车时间为
 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 元,分别求出
元,分别求出 ,
, 关于
关于 的函数表达式;
的函数表达式;(2)请你帮助小明计算并选择哪个出游方案合算。
相关试题

