【题目】如图,将一个正方形纸片OABC放置在平面直角坐标系中,其中A(1,0),C(0,1),P为AB边上一个动点,折叠该纸片,使O点与P点重合,折痕l与OP交于点M,与 对角线AC交于Q点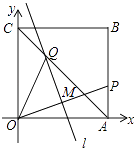
(Ⅰ)若点P的坐标为(1, ![]() ),求点M的坐标;
),求点M的坐标;
(Ⅱ)若点P的坐标为(1,t)
①求点M的坐标(用含t的式子表示)(直接写出答案)
②求点Q的坐标(用含t的式子表示)(直接写出答案)
(Ⅲ)当点P在边AB上移动时,∠QOP的度数是否发生变化?如果你认为不发生变化,写出它的角度的大小.并说明理由;如果你认为发生变化,也说明理由.
参考答案:
【答案】解:(Ⅰ)过M作ME⊥x轴于点E,如图1,
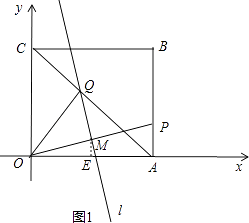
由题意可知M为OP中点,
∴E为OA中点,
∴OE= ![]() OA=
OA= ![]() ,ME=
,ME= ![]() AP=
AP= ![]() ,
,
∴M点坐标为( ![]() ,
, ![]() );
);
(Ⅱ)①同(Ⅰ),当P(1,t)时,可得M( ![]() ,
, ![]() t);
t);
②过Q点作QD⊥OA于D,作QE⊥AB与E,连接QP. 
∵Q点在AC上,
∴QD=AD=AE=QE,
在Rt△OQD和Rt△OPE中,
![]()
∴Rt△OQD≌Rt△OPE,
∴OD=PE,
设OD=PE=x,则AD=1﹣x,AE=t+x,则1﹣x=t+x,解得x= ![]() ,
,
QD=AE=t+x= ![]() .
.
∴Q点坐标为( ![]() ,
, ![]() ).
).
(Ⅲ)不变化,∠QOP=45°.
理由如下:由(Ⅱ)②可知Q点坐标为( ![]() ,
, ![]() ),
),
根据勾股定理得,
OQ2=OD2+QD2=( ![]() )2+(
)2+( ![]() )2=
)2= ![]() ,
,
QP=OQ,
OP2=OA2+AP2=1+t2,
∴OQ2+QP2=OP2,
∴△OPQ是以OP为斜边的等腰直角三角形,
∴∠QOP=45°,
即∠QOP不变化.
【解析】(Ⅰ)由题意可知M为OP中点,得到E为OA中点,得到M点坐标为(![]() ,
,![]() );(Ⅱ)①同(Ⅰ),当P(1,t)时,可得M(
);(Ⅱ)①同(Ⅰ),当P(1,t)时,可得M(![]() ,
,![]() t);②由题意得到QD=AD=AE=QE,Rt△OQD≌Rt△OPE,OD=PE,得到Q点坐标为(
t);②由题意得到QD=AD=AE=QE,Rt△OQD≌Rt△OPE,OD=PE,得到Q点坐标为(![]() ,
, ![]() );(Ⅲ)由(Ⅱ)②可知Q点坐标,根据勾股定理得到OQ2+QP2=OP2,所以△OPQ是以OP为斜边的等腰直角三角形,∠QOP不变化;此题是综合题,难度较大,计算和解方程时需认真仔细.
);(Ⅲ)由(Ⅱ)②可知Q点坐标,根据勾股定理得到OQ2+QP2=OP2,所以△OPQ是以OP为斜边的等腰直角三角形,∠QOP不变化;此题是综合题,难度较大,计算和解方程时需认真仔细.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y =
 x,过点A(0,1)作y轴的垂线交直线
x,过点A(0,1)作y轴的垂线交直线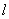 于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2019的坐标为( )
于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2019的坐标为( )
A. (0,42019) B. (0,42018) C. (0,32019) D. (0,32018)
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m,先到终点
的人原地休息.已知甲先出发2s.在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系
如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是【 】

A.①②③ B.仅有①② C.仅有①③ D.仅有②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′,利用网格点画图和无刻度的直尺画图并解答(保留画图痕迹):
(1)画出△A′B′C′;
(2)画出△ABC的高,即线段BD;
(3)连接AA′、 CC′,那么AA′与CC′的关系是________;线段AC扫过图形的面积为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图1中的长方形长为宽的3倍,将四个这样的长方形拼成图2中的大正方形.
(1)若中间小正方形的面积是
 ,问图1中的长方形的面积是多少
,问图1中的长方形的面积是多少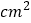 ?
? (2)若大正方形的面积就比小正方形的面积大
 ,求中间小正方形的面积.
,求中间小正方形的面积.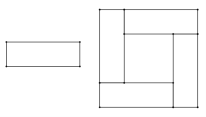
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1为深50cm的圆柱形容器,底部放入一个长方体的铁块,现在以一定的速度向容器内注水,图2为容器顶部离水面的距离y(cm)随时间t(分钟)的变化图象,则( )
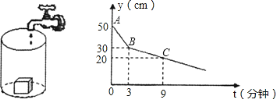
A. 注水的速度为每分钟注入
 cm高水位的水
cm高水位的水B. 放人的长方体的高度为30cm
C. 该容器注满水所用的时间为21分钟
D. 此长方体的体积为此容器的体积的0.35.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).

(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.
相关试题

