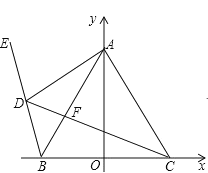
【题目】如图,已知 B 1, 0 , C 1, 0 , A 为 y 轴正半轴上一点, AB AC ,点 D 为第二象限一动点,E 在 BD 的延长线上, CD 交 AB 于 F ,且BDC BAC .
(1)求证: ABD ACD ;
(2)求证: AD 平分CDE ;
(3)若在 D 点运动的过程中,始终有 DC DA DB ,在此过程中,BAC 的度数是否变化?如果变化,请说明理由;如果不变,请求出BAC 的度数?
参考答案:
【答案】(1)见解析;(2)见解析;(3)∠BAC的度数不变化.∠BAC=60°.
【解析】
(1)根据三角形内角和定理等量代换可得结论;(2)作AM⊥CD于点M,作AN⊥BE于点N,证明△ACM≌△ABN即可;(3)用截长补短法在CD上截取CP=BD,连接AP,证明△ABD≌△ACP,由全等性质可知△ADP是等边三角形,易知BAC 的度数.
(1)∵∠BDC=∠BAC,∠DFB=∠AFC,
又∵∠ABD+∠BDC+∠DFB=∠BAC+∠ACD+∠AFC=180°,
∴∠ABD=∠ACD;
(2)过点A作AM⊥CD于点M,作AN⊥BE于点N.
则∠AMC=∠ANB=90°.
∵OB=OC,OA⊥BC,
∴AB=AC,
∵∠ABD=∠ACD,
∴△ACM≌△ABN (AAS)
∴AM=AN.
∴AD平分∠CDE.(到角的两边距离相等的点在角的平分线上);
(3)∠BAC的度数不变化.
在CD上截取CP=BD,连接AP.

∵CD=AD+BD,
∴AD=PD.
∵AB=AC,∠ABD=∠ACD,BD=CP,
∴△ABD≌△ACP.
∴AD=AP;∠BAD=∠CAP.
∴AD=AP=PD,即△ADP是等边三角形,
∴∠DAP=60°.
∴∠BAC=∠BAP+∠CAP=∠BAP+∠BAD=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
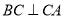 ,
,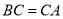 ,
,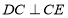 ,
, ,直线
,直线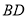 与
与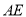 交于点
交于点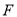 ,交
,交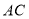 于点
于点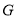 ,连接
,连接 .
.
(1)求证:
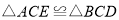 ;
;(2)求证:
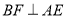 ;
;(3)请判断
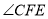 与
与 的大小关系并说明理由.
的大小关系并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三位数,十位数字等于百位数字与个位数字的平均数,我们称这个三位数为“顺子数”,例如:630,123.
如果一个三位数,十位数字等于百位数字与个位数字的积的算术平方根,我们称这个三位数为“和谐数”,例如:139,124.
(1)若三位数
 是“顺子数”,且各位数字之和大于7小于10,且百位数字a使得一元二次方程(a﹣5)x2+2ax+a﹣6=0有实数根,求这个“顺子数”;
是“顺子数”,且各位数字之和大于7小于10,且百位数字a使得一元二次方程(a﹣5)x2+2ax+a﹣6=0有实数根,求这个“顺子数”;(2)若三位数
 既是“顺子数”又是“和谐数”,请探索a,b,c三者的关系.
既是“顺子数”又是“和谐数”,请探索a,b,c三者的关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 在
在 的
的 边上,
边上, 交
交 于
于 ,
, 交
交 于
于 ,若添加条件________,则四边形
,若添加条件________,则四边形 是矩形;若添加条件________,则四边形
是矩形;若添加条件________,则四边形 是菱形;若添加条件________,则四边形
是菱形;若添加条件________,则四边形 是正方形.
是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动–探究特殊的平行四边形.
问题情境
如图,在四边形
 中,
中, 为对角线,
为对角线, ,
, .请你添加条件,使它们成为特殊的平行四边形.
.请你添加条件,使它们成为特殊的平行四边形.提出问题

 第一小组添加的条件是“
第一小组添加的条件是“ ”,则四边形
”,则四边形 是菱形.请你证明;
是菱形.请你证明; 第二小组添加的条件是“
第二小组添加的条件是“ ,
, ”,则四边形
”,则四边形 是正方形.请你证明.
是正方形.请你证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,若
,若 ,则还需添加的一个条件有( )
,则还需添加的一个条件有( )

A.
 种B.
种B. 种C.
种C.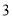 种D.
种D. 种
种 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,完成下列推理过程:
如图所示,点E在
 外部,点D在BC边上,DE交AC于F,若
外部,点D在BC边上,DE交AC于F,若 ,
,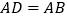 ,
,求证:
 .
.
证明:∵
 (已知),
(已知), (________________),
(________________),∴
 (________________),
(________________),又∵
 ,
,∴________
 ________
________ (________),
(________),即
 ,
,在
 和
和 中
中 (已证)
(已证)∵
 (已知)
(已知) (已证)
(已证)∴
 (________).
(________).∴
 (________________)
(________________)
相关试题

