【题目】如图,完成下列推理过程:
如图所示,点E在![]() 外部,点D在BC边上,DE交AC于F,若
外部,点D在BC边上,DE交AC于F,若![]() ,
,![]() ,
,
求证:![]() .
.

证明:∵![]() (已知),
(已知),
![]() (________________),
(________________),
∴![]() (________________),
(________________),
又∵![]() ,
,
∴________![]() ________
________![]() (________),
(________),
即![]() ,
,
在![]() 和
和![]() 中
中
![]() (已证)
(已证)
∵![]() (已知)
(已知)
![]() (已证)
(已证)
∴![]() (________).
(________).
∴![]() (________________)
(________________)
参考答案:
【答案】对顶角相等,三角形内角和![]() ,
,![]() ,
,![]() ,等式性质,AAS,三角形全等,对应边相等
,等式性质,AAS,三角形全等,对应边相等
【解析】
首先证明![]() ,再证明∠BAC=∠DAE,进而可利用AAS判定三角形全等即可.
,再证明∠BAC=∠DAE,进而可利用AAS判定三角形全等即可.
证明:∵![]() (已知),
(已知),
![]() (对顶角相等),
(对顶角相等),
∴![]() (三角形内角和
(三角形内角和![]() ),
),
又∵![]() ,
,
∴![]()
![]()
![]() _
_![]() (等式性质),
(等式性质),
即![]() ,
,
在![]() 和
和![]() 中
中
![]() (已证)
(已证)
∵![]() (已知)
(已知)
![]() (已证)
(已证)
∴![]() (AAS).
(AAS).
∴![]() (三角形全等,对应边相等)
(三角形全等,对应边相等)
-
科目: 来源: 题型:
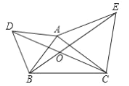
查看答案和解析>>【题目】如图,
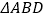 与
与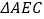 都是等边三角形,
都是等边三角形,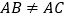 ,下列结论中,正确的个数是( )①
,下列结论中,正确的个数是( )①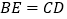 ;②
;②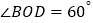 ;③
;③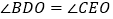 ;④若
;④若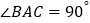 ,且
,且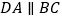 ,则
,则 .
.
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知点A、B是反比例函数y=﹣
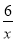 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知点A、B是反比例函数y=﹣
 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
【答案】

【解析】过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,如图所示.

∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,由
 ,
,∴△ACD≌△CBE(ASA).
设点B的坐标为(m,﹣
 )(m<0),则E(0,﹣
)(m<0),则E(0,﹣ ),点D(0,3﹣m),点A(﹣
),点D(0,3﹣m),点A(﹣ ﹣3,3﹣m),
﹣3,3﹣m),∵点A(﹣
 ﹣3,3﹣m)在反比例函数y=﹣
﹣3,3﹣m)在反比例函数y=﹣ 上,
上, ,解得:m=﹣3,m=2(舍去).
,解得:m=﹣3,m=2(舍去).∴点A的坐标为(﹣1,6),点B的坐标为(﹣3,2),点F的坐标为(﹣1,2),
∴BF=2,AF=4,

故答案为:2
 .
.【点睛】
过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,根据角的计算得出“∠ACD=∠CBE,∠BCE=∠CAD”,由此证出△ACD≌△CBE;再设点B的坐标为(m,﹣
 ),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.【题型】填空题
【结束】
18【题目】二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
【答案】

【解析】试题解析:∵二次函数有最小值﹣2,
∴y=﹣
 ,
,解得:m=
 .
.【题型】填空题
【结束】
19【题目】如图,已知△ABC三个顶点的坐标分别是A(-2,3),B(-3,-1),C(-1,1)

(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转180°后的△A2B2C2,并写出点A2的坐标;
(3)直接回答:∠AOB与∠A2OB2有什么关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
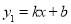 和
和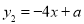 的图象如图所示,且
的图象如图所示,且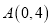 ,
,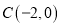 .
.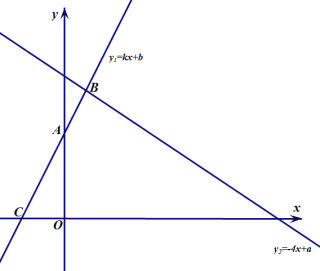
(1)由图可知,不等式
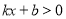 的解集是______;
的解集是______;(2)若不等式
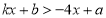 的解集是
的解集是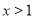 .
.①点
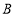 的坐标为______.
的坐标为______.②
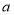 的值为_______.
的值为_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC三个顶点的坐标分别是A(-2,3),B(-3,-1),C(-1,1)
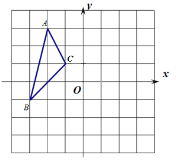
(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转180°后的△A2B2C2,并写出点A2的坐标;
(3)直接回答:∠AOB与∠A2OB2有什么关系?
【答案】(1)作图见解析,(-4,-2);(2)作图见解析,(2,-3);(3)相等.
【解析】
试题分析:(1)根据旋转的性质作图,写出点的坐标;
根据旋转的性质作图,写出点的坐标;
(3)根据旋转的性质得出结论.
试题解析:(1)作图如下,点A1的坐标(-4,-2).
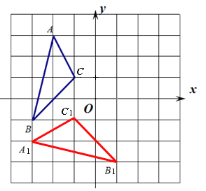
(2)作图如下,点A2的坐标(2,-3).
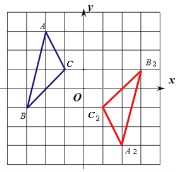
(3)相等.
考点:1.旋转作图;2.旋转的性质.
【题型】解答题
【结束】
20【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
相关试题

