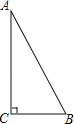
【题目】如图,△ABC是直角三角形,∠ACB=90°.
(1)动手操作:利用尺规作∠ABC的平分线,交AC于点O,再以O为圆心,OC的长为半径作⊙O(保留作图痕迹,不写作法);
(2)综合运用:在你所作的图中,
①判断AB与⊙O的位置关系,并证明你的结论;
②若AC=12,tanOBC=![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】(1)见解析;(2)AB与⊙O相切,理由见解析;(3)![]()
【解析】试题分析:(1)只需按照题目的要求画图即可;
(2)①过点O作OD⊥AB,垂足为D,如图所示,只需证明OD=OC即可;②在Rt△OBC中,运用三角函数可求出![]() ,从而得到
,从而得到![]() ,易证Rt△ADO∽Rt△ACB,运用相似三角形的性质可求得AD=8,然后在Rt△ADO中运用勾股定理即可解决问题.
,易证Rt△ADO∽Rt△ACB,运用相似三角形的性质可求得AD=8,然后在Rt△ADO中运用勾股定理即可解决问题.
试题解析:(1)如图,⊙O即为所求作;

(2)AB与⊙O相切,理由如下:
过点O作OD⊥AB,垂足为D,如图所示.
∵∠ACB=90°,∴OC⊥BC.
∵BO是∠ABC的平分线,OD⊥AB,OC⊥BC,
∴OC=OD.
∴AB与⊙O相切;
(3)在Rt△OBC中,
tan∠OBC=![]()
∴![]() .
.
又∵∠ADO=∠ACB=90°,∠A=∠A,
∴Rt△ADO∽Rt△ACB,
∴![]() ,
,
∴AD=![]() AC=
AC=![]() ×12=8.
×12=8.
设⊙O的半径为r,则OD=OC=r,AO=12-r.
在Rt△ADO中,
根据勾股定理可得r2+82=(12-r)2,
解得r=![]() ,
,
∴⊙O的半径是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某数学兴趣小组在本校学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查结果,绘制了如图的统计图,结合统计图,回答下列问题.
(1)本次抽样调查的样本容量是;
(2)若该校有学生1500人,请根据调查结果估计这些学生中“比较了解”雾霾天气知识的人数约为多少?
(3)根据调查结果,学校准备开展关于雾霾天气知识竞赛,某班要从“非常了解”的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:在一个不透明的袋中装有2个红球和2个白球,它们除了颜色外无其它差别,从中随机摸出两个球,若摸出的两个球颜色相同,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知P(x,y)在第二象限,且x2=4,|y|=7,则点P的坐标是( )
A.(2,﹣7)
B.(﹣4,7)
C.(4,﹣7)
D.(﹣2,7) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC 中的∠B=∠A+10°,∠C=∠B+10°,则∠A=_____,∠B=_____,∠C=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一数值转换器,原理如图所示,若开始输入x的值是14,可发现第1次输出的结果是7,第2次输出的结果是12,依次继续下去,则第2015次输出的结果是_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二元一次方程x+3y=7的正整数解的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AEAD=AHAF;其中结论正确的个数是()
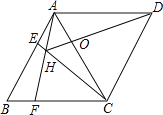
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

