【题目】(1)如图1,AB∥CD,∠A=35°,∠C=40°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在射线DM上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.

参考答案:
【答案】(1)∠APC=75°;(2)∠APC=∠α+∠β,见解析;(3)∠APC=∠α-∠β.
【解析】
(1)过点P作PE∥AB,通过平行线性质来求∠APC.
(2)过P作PE∥AD交AC于E,推出AB∥PE∥DC,根据平行线的性质得出∠α=∠APE,∠β=∠CPE,即可得出答案;
(3)若P在BD延长线上,画出图形,根据平行线的性质得出∠α=∠APE,∠β=∠CPE,依据角的和差关系即可得出答案.
解:(1)如图1,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A=∠APE,∠C=∠CPE,
∵∠A=35°,∠C=40°,
∴∠APE=35°,∠CPE=40°,
∴∠APC=∠APE+∠CPE=35°+40°=75°;
(2)∠APC=∠α+∠β,
理由是:如图2,过P作PE∥AB,交AC于E,
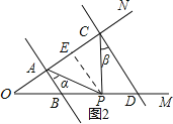
∵AB∥CD,
∴AB∥PE∥CD,
∴∠APE=∠PAB=∠α,∠CPE=∠PCD=∠β,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图3,过P作PE∥AB,交AC于E,
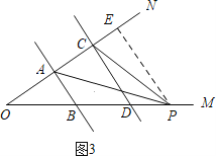
∵AB∥CD,
∴AB∥PE∥CD,
∴∠PAB=∠APE=∠α,∠PCD=∠CPE=∠β,
∵∠APC=∠APE-∠CPE,
∴∠APC=∠α-∠β.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
 ,
, ,
, ,
, ,…,则第8个等式是__________.
,…,则第8个等式是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】完善下列解题步骤,并说明解题依据.
如图,已知
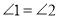 ,
,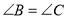 ,求证:
,求证: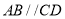
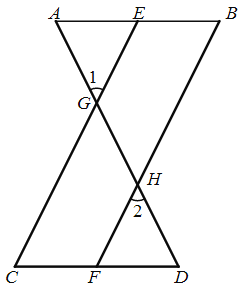
证明:
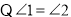 (已知),
(已知),且
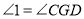 (_____________________),
(_____________________),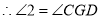 (_____________________),
(_____________________), (_____)
(_____)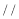 (______)(________________),
(______)(________________),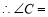 (______)(______________________),
(______)(______________________),又
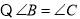 (已知),
(已知), (_______)
(_______)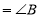
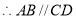 (___________________).
(___________________). -
科目: 来源: 题型:
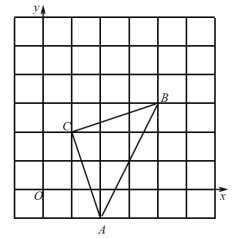
查看答案和解析>>【题目】如图,直角坐标系中,
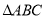 的顶点都在网格点上,其中,
的顶点都在网格点上,其中, 点坐标为
点坐标为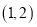 ,
,
(1)写出点
 、
、 的坐标:
的坐标: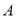 (____,____)、
(____,____)、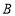 (____,____)
(____,____)(2)将
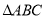 先向左平移
先向左平移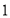 个单位长度,再向上平移
个单位长度,再向上平移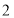 个单位长度,得到
个单位长度,得到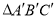 ,画出
,画出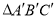 ;
;(3)写出三个顶点坐标
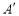 (___,___)、
(___,___)、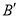 (___,___)、
(___,___)、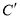 (___,___);
(___,___);(4)求
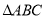 的面积.
的面积. -
科目: 来源: 题型:
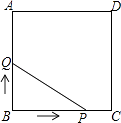
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.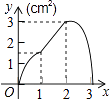
B.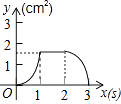
C.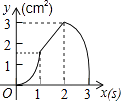
D.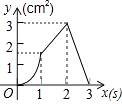
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图长方形
 的位置如图所示,点
的位置如图所示,点 的坐标为
的坐标为 ,点
,点 从点
从点 出发向点
出发向点 移动,速度为每秒
移动,速度为每秒 个单位;点
个单位;点 同时从点
同时从点 出发向点
出发向点 移动,速度为每秒
移动,速度为每秒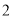 个单位.
个单位.
(1)请写出点
 、
、 的坐标.
的坐标.(2)经过几秒后,
 、
、 两点与原点距离相等.
两点与原点距离相等.(3)在点
 、
、 移动过程中,四边形
移动过程中,四边形 的面积有何变化,说明理由.
的面积有何变化,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明今年五一节去三峡广场逛水果超市,他分两次购进了
 、
、 两种不同单价的水果.第一次购买
两种不同单价的水果.第一次购买 种水果的数量比
种水果的数量比 种水果的数量多50%,第二次购买
种水果的数量多50%,第二次购买 种水果的数量比第一次购买
种水果的数量比第一次购买 种水果的数量少60%,结果第二次购买水果的总数量比第一次购买水果的总数量多20%,且第二次购买
种水果的数量少60%,结果第二次购买水果的总数量比第一次购买水果的总数量多20%,且第二次购买 、
、 水果的总费用比第一次购买
水果的总费用比第一次购买 、
、 水果的总费用少10%(两次购买中
水果的总费用少10%(两次购买中 、
、 两种水果的单价不变),则
两种水果的单价不变),则 种水果的单价与
种水果的单价与 种水果的单价的比值是______.
种水果的单价的比值是______.
相关试题

