【题目】如图,在数轴上点A所表示的数是![]() ,点B在点A的右侧,AB=6;点C在AB之间, AC=2BC.
,点B在点A的右侧,AB=6;点C在AB之间, AC=2BC.
(1)在数轴上描出点B;
(2)求点C所表示的数,并在数轴上描出点C;
(3)已知在数轴上存在点P,使PA+PC=PB,求点P所表示的数.
![]()
参考答案:
【答案】(1)见解析;(2)-1,图见解析;(3)-3或-7.
【解析】
(1)根据点A和AB之间的距离即可找到点B的位置;
(2)解法一:根据AC=2BC和AB=6求出B、C之间的距离,再利用点B的位置即可得出点C所表示的数;
解法二:利用方程的思想,将BC设为x,通过AB=6建立一个关于x的方程并解方程,再利用点B的位置即可得出点C所表示的数;
解法三:设点C所表示的数为x,将AC,BC表示出来,建立方程求解即可;
(3)解法一:因为PA+PC=PB,分①当点P在AC之间时,②当点P在点A左侧时两种情况分情进行讨论即可;
解法二:利用PA =PB-PC=BC=2直接找到A,P之间的距离即可得出答案.
解:(1)点B在数轴上的位置如图1所示.
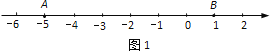
(2)解法一:因为AC=2BC,点C在AB之间,
所以AB=AC+BC=3BC.
因为AB=1-(-5)=6,
所以BC=2.
因为点B所表示的数是1,
1-2=-1
所以点C所表示的数是-1.
解法二:设BC=x,则AC=2x.
因为AB=1-(-5)=6,
所以x+2x=6.
解得x=2.
因为点B所表示的数是1,
1-2=-1
所以点C所表示的数是-1.
解法三:设点C所表示的数为x.
因为点C在AB之间,
所以BC=1-x,AC=x-(-5)= x +5.
因为AC=2BC,
所以x +5=2(1-x).
解得x=-1
点C在数轴上的位置如图2所示.
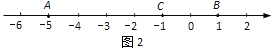
(3)解法一:因为PA+PC=PB,
所以点P在点C左侧.
因为点A表示的数是-5,点B表示的数是1,点C表示的数是-1,
所以AC =-1-(-5)=4,AB=1-(-5)=6.
①当点P在AC之间时,
设PA=x,则PC = AC- PA =4-x.
所以PB=PC+ BC =4-x +2=6-x.
因为PA+PC=PB,
所以x+4-x=6-x.
解得 x=2.
因为点A所表示的数是-5,-5+2=-3,
此时点P所表示的数是-3.
②当点P在点A左侧时,
设PA=x,则PC = PA+ AC =4+x,PB=PA+ AB =x +6,
因为PA+PC=PB,
所以x+4+x=6+x.
解得 x=2.
因为点A所表示的数是-5,-5-2=-7,
此时点P所表示的数是-7.
所以点P所表示的数是-3或-7.
解法二:因为PA+PC=PB,
所以点P在点C左侧.
所以PA =PB-PC=BC=2.
因为点A所表示的数是-5,
所以点P所表示的数是-3或-7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在精准扶贫政策的扶持下,贫困户老李今年试种的百香果获得大丰收,共收获2 000千克.扶贫小组帮助他将百香果按照品质从高到低分成A,B,C,D,E五个等级,并根据数据绘制了如下的扇形统计图和频数分布表:

请根据图表信息解答下列问题:
(1)
 __________;
__________; __________;
__________; __________;
__________;(2)求扇形统计图中“E”所对应的圆心角的度数;
(3)为了帮助贫困户老李销售百香果,扶贫小组联系了甲、乙两位经销商.他们分别给出如下收购方案:
甲:全部按5元/千克收购;
乙:按等级收购:C等级单价为6.5元/千克,每提高一个等级单价提高1元/千克,剩下的D,E两个等级单价均为2元/千克.
请你通过计算,判断哪个经销商的方案使老李盈利更多.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=
 ,求AB的长。
,求AB的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.

(1)求证:△ADG≌△CDG.
(2)若
 =
= ,EG=4,求AG的长.
,EG=4,求AG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
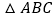 中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且
中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且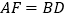 ,连接BF.
,连接BF.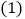 证明:
证明: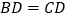 ;
;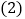 当
当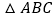 满足什么条件时,四边形AFBD是矩形?并说明理由.
满足什么条件时,四边形AFBD是矩形?并说明理由.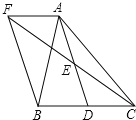
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,将线段EF绕点F旋转,使点E落在BE上的点G处,连接CG.
(1)证明:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积;
(3)试探究当线段AB与BC满足什么数量关系时,BG=CG,请写出你的探究过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
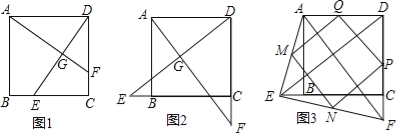
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
相关试题

