【题目】如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,将线段EF绕点F旋转,使点E落在BE上的点G处,连接CG.
(1)证明:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积;
(3)试探究当线段AB与BC满足什么数量关系时,BG=CG,请写出你的探究过程.

参考答案:
【答案】(1)见解析;(2)20;(3)![]()
【解析】试题分析:(1)由折叠得到EF=CE,∠FEG=∠CEG,再加上公共边GE,利用SAS可得出△EFG≌△ECG,利用全等三角形的对应边相等可得出GF=CG,再由FG是线段EF旋转得到的,故FG=EF,等量代换可得出四边形EFGC四条边相等,进而确定出此四边形为菱形;(2)连接FC,与GE交于点O,由折叠得到BF=BC=10,连接FC,交GE于O点,在Rt△ABF中,根据勾股定理求得AF =6,即可得FD=4,设EC=x,则DE=8-x,EF=x,在Rt△FDE中利用勾股定理列出方程42+(8-x)2=x2,解方程得EC=5;在Rt△FDC中根据勾股定理求得FC=4![]() ;在菱形FGCE中FO=
;在菱形FGCE中FO=![]() FC=2
FC=2![]() ,EO=
,EO=![]() GE,GE⊥FC,在在Rt△FOE中求得EO=
GE,GE⊥FC,在在Rt△FOE中求得EO=![]() ,即可得GE=2EO=2
,即可得GE=2EO=2![]() ,从而根据菱形的面积等于两条对角线乘积的一半即可求得菱形的面积;(3)当线段AB与BC满足
,从而根据菱形的面积等于两条对角线乘积的一半即可求得菱形的面积;(3)当线段AB与BC满足![]() 时,BG=CG,理由为:在Rt△ABF中,利用特殊角的三角函数值及锐角三角函数定义求出∠ABF的度数,进而确定出∠FBC的度数,再由折叠得到∠FBE=∠EBC,求出∠EBC为30°,可得出∠BEC为60°,再由GC=CE得到△CGE为等边三角形,再由30°所对的直角边EC等于斜边BE的一半,得到GE为BE的一半,即G为BE的中点,利用直角三角形斜边上的中线等于斜边的一半,得到CG与BG相等都为BE的一半.
时,BG=CG,理由为:在Rt△ABF中,利用特殊角的三角函数值及锐角三角函数定义求出∠ABF的度数,进而确定出∠FBC的度数,再由折叠得到∠FBE=∠EBC,求出∠EBC为30°,可得出∠BEC为60°,再由GC=CE得到△CGE为等边三角形,再由30°所对的直角边EC等于斜边BE的一半,得到GE为BE的一半,即G为BE的中点,利用直角三角形斜边上的中线等于斜边的一半,得到CG与BG相等都为BE的一半.
试题解析:
(1)根据翻折的方法可得:EF=EC,∠FEG=∠CEG,
在△EFG和△ECG中,
∵ ,
,
∴△EFG≌△ECG(SAS),
∴FG=GC,
∵线段FG是由EF绕F旋转得到的,
∴EF=FG,
∴EF=EC=FG=GC,
∴四边形FGCE是菱形;
(2)连接FC,交GE于O点,

根据折叠可得:BF=BC=10,
∵AB=8,
在Rt△ABF中,
根据勾股定理得:AF=![]() =6,
=6,
∴FD=AD-AF=10-6=4,
设EC=x,则DE=8-x,EF=x,
在Rt△FDE中:FD2+DE2=EF2,即42+(8-x)2=x2,
解得:x=5,
在Rt△FDC中:FD2+DC2=CF2,
则:42+82=FC2,
解得:FC=4![]() ,
,
∵四边形FGCE是菱形,
∴FO=![]() FC=2
FC=2![]() ,EO=
,EO=![]() GE,GE⊥FC,
GE,GE⊥FC,
在Rt△FOE中:FO2+OE2=EF2,即(2![]() )2+EO2=52,
)2+EO2=52,
解得:EO=![]() ,
,
∴GE=2EO=2![]() ,
,
则S菱形CEFG=![]() ×FC×GE=
×FC×GE=![]() ×4
×4![]() ×2
×2![]() =20;
=20;
(3)当![]() 时,BG=CG,理由为:
时,BG=CG,理由为:
由折叠可得:BF=BC,∠FBE=∠CBE,
∵在Rt△ABF中, ![]() ,
,
∴cos∠ABF=![]() ,即∠ABF=30°,
,即∠ABF=30°,
又∵∠ABC=90°,
∴∠FBC=60°,EC=![]() BE,
BE,
∴∠FBE=∠CBE=30°,
∵∠BCE=90°,
∴∠BEC=60°,
又∵GC=CE,
∴△GCE为等边三角形,
∴GE=CG=CE=![]() BE,
BE,
∴G为BE的中点,
则CG=BG=![]() BE.
BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.

(1)求证:△ADG≌△CDG.
(2)若
 =
= ,EG=4,求AG的长.
,EG=4,求AG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A所表示的数是
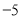 ,点B在点A的右侧,AB=6;点C在AB之间, AC=2BC.
,点B在点A的右侧,AB=6;点C在AB之间, AC=2BC.(1)在数轴上描出点B;
(2)求点C所表示的数,并在数轴上描出点C;
(3)已知在数轴上存在点P,使PA+PC=PB,求点P所表示的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
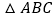 中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且
中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且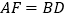 ,连接BF.
,连接BF.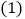 证明:
证明: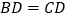 ;
;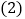 当
当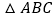 满足什么条件时,四边形AFBD是矩形?并说明理由.
满足什么条件时,四边形AFBD是矩形?并说明理由.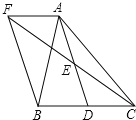
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
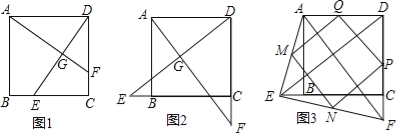
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=2x2+bx+c经过点A(2,-1) .
(1)若抛物线的对称轴为x=1,求b,c的值;
(2)求证:抛物线与x轴有两个不同的交点;
(3)设抛物线顶点为P,若O、A、P三点共线(O为坐标原点),求b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格(边长为1的小正方形组成的网格纸,正方形的顶点称为格点)是我们在初中阶段常用的工具,利用它可以解决很多问题.
(1)如图①中,△ABC是格点三角形(三个顶点为格点),则它的面积为 ;
(2)如图②,在4×4网格中作出以A为顶点,且面积最大的格点正方形(四个顶点均为格点);
(3)人们发现,记格点多边形(顶点均为格点)内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb-1,其中m,n为常数.试确定m,n的值.

相关试题

