【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D. 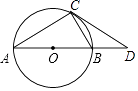
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB= ![]() CD,求⊙O半径.
CD,求⊙O半径.
参考答案:
【答案】
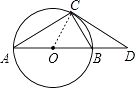
(1)证明:如图,连接CO,
 ,
,
∵CD与⊙O相切于点C,
∴∠OCD=90°,
∵AB是圆O的直径,
∴∠ACB=90°,
∴∠ACO=∠BCD,
∵∠ACO=∠CAD,
∴∠CAD=∠BCD,
在△ADC和△CDB中,
![]()
∴△ADC∽△CDB.
(2)解:设CD为x,
则AB= ![]() x,OC=OB=
x,OC=OB= ![]() x,
x,
∵∠OCD=90°,
∴OD= ![]() =
= ![]() =
= ![]() x,
x,
∴BD=OD﹣OB= ![]() x﹣
x﹣ ![]() x=
x= ![]() x,
x,
由(1)知,△ADC∽△CDB,
∴ ![]() =
= ![]() ,
,
即 ![]() ,
,
解得CB=1,
∴AB= ![]() =
= ![]() ,
,
∴⊙O半径是 ![]()
【解析】(1)首先连接CO,根据CD与⊙O相切于点C,可得:∠OCD=90°;然后根据AB是圆O的直径,可得:∠ACB=90°,据此判断出∠CAD=∠BCD,即可推得△ADC∽△CDB.(2)首先设CD为x,则AB= ![]() x,OC=OB=
x,OC=OB= ![]() x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得:
x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得: ![]() =
= ![]() ,据此求出CB的值是多少,即可求出⊙O半径是多少.
,据此求出CB的值是多少,即可求出⊙O半径是多少.
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程
已知a、b、c为△ABC为三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状
解:∵a2c2-b2c2=a4-b4①
∴c2(a2-b2)=(a2-b2)(a2+b2)②
∴c2=a2+b2③
∴△ABC是直角三角形
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的序号________.
(2)错误原因为________.
(3)本题正确结论是什么,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知数轴上点A、B分别表示a、b,且|b+6|与(a﹣9)2互为相反数,O为原点.
(1)a= ,b= ;
(2)若将数轴折叠点A与表示﹣10的点重合,则与点B重合的点所表示的数为 ;
(3)若点M、N分别从点A、B同时出发,点M以每秒1个单位长度的速度沿数轴向左匀速运动,点N以每秒2个单位长度的速度沿数轴向右匀速运动,N到点A后立刻原速返回,设运动时间为t(t>0)秒.①点M表示的数是 (用含t的代数式表示);②求t为何值时,2MO=MA;③求t为何值时,点M与N相距3个单位长度.
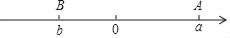
-
科目: 来源: 题型:
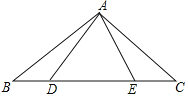
查看答案和解析>>【题目】如图,点D,E在△ABC的边BC上,连接AD,AE.有下面三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成三个命题.解答下列问题
(1)写出这三个命题,并直接判断其是否是真命题;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
-
科目: 来源: 题型:
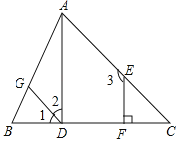
查看答案和解析>>【题目】如图,已知EF⊥BC,∠1=∠C,∠2+∠3=180°.试说明直线AD与BC垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某重点中学校团委、学生会发出倡议,在初中各年级捐款购买书籍送给我市贫困地区的学校.初一年级利用捐款买甲、乙两种自然科学书籍若干本,用去5324元;初二年级买了A、B两种文学书籍若干本,用去4840元,其中A、B的数量分别与甲、乙的数量相等,且甲种书与B种书的单价相同,乙种书与A种书的单价相同.若甲、乙两种书的单价之和为121元,则初一和初二两个年级共向贫困地区的学校捐献了________本书.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列定义一种关于n的运算:①当n是奇数时,结果为3n+5 ②n为偶数时结果是
 (其中k是使
(其中k是使 是奇数的正整数),并且运算重复进行.例如:取n=26,则…,若n=449,则第449次运算结果是( )
是奇数的正整数),并且运算重复进行.例如:取n=26,则…,若n=449,则第449次运算结果是( )A. 1 B. 2 C. 7 D. 8
相关试题

