【题目】阅读下列推理过程,在括号中填写理由.
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
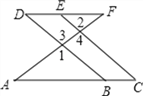
解:∵∠1=∠2(已知),∠1=∠3(______________),
∴∠2=∠3(___________________).
∴__∥__(__________________________________).
∴∠C=∠ABD (________________________________).
又∵∠C=∠D(____________),
∴∠D=∠ABD(等量代换)
∴AC∥DF(______________________________).
参考答案:
【答案】 对顶角相等; 等量代换; EC; BD; 内错角相等,两直线平行; 两直线平行,同位角相等; 已知; 内错角相等,两直线平行。
【解析】分析: 分析:先证明BD∥CE,然后根据平行线的性质,以及已知条件证明∠D=∠ABD,根据同位角相等,两直线平行即可证得.
本题解析:
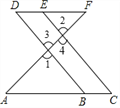
∵∠1=∠2,(已知)∠1=∠3(对顶角相等)
∴∠2=∠3,(等量代换)
∴DB∥EC,(同位角相等,两直线平行)
∴∠C=∠ABD,(两直线平行,同位角相等)
又∵∠C=∠D,(已知)
∴∠D=∠ABD,(等量代换)
∴AC∥DF.(内错角相等,两直线平行)
-
科目: 来源: 题型:
查看答案和解析>>【题目】要证明一个三角形中不可能有两个钝角,采用的方法是 ,应先假设
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于命题“如果a=b,那么ac=bc.”,它的逆命题是________命题.(填“真”或“假”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣x﹣2=0的解是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,AB=10,AC=8,点Q在AB上,且AQ=2,过Q做QR⊥AB,垂足为Q,QR交折线AC﹣CB于R(如图1),当点Q以每秒2个单位向终点B移动时,点P同时从A出发,以每秒6个单位的速度沿AB﹣BC﹣CA移动,设移动时间为t秒(如图2).
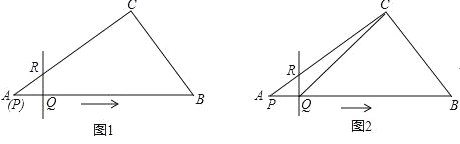
(1)求△BCQ的面积S与t的函数关系式.
(2)t为何值时,QP∥AC?
(3)t为何值时,直线QR经过点P?
(4)当点P在AB上运动时,以PQ为边在AB上方所作的正方形PQMN在Rt△ABC内部,求此时t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州市甲、乙两个有名的学校乐团,决定向某服装厂购买同样的演出服.如表是服装厂给出的演出服装的价格表:
购买服装的套数
1~39套(含39套)
40~69套(含69套)
70套及以上
每套服装的价格
80元
70元
60元
经调查:两个乐团共85人(甲乐团人数不少于46人),如果分别各自购买演出服,两个乐团共需花费6500元.请回答以下问题:
(1)如果甲、乙两个乐团联合起来购买服装,那么比各自购买服装最多可以节省多少元?
(2)甲、乙两个乐团各有多少名学生?
(3)现从甲乐团抽调a人,从乙乐团抽调b人(要求从每个乐团抽调的人数不少于5人),去儿童福利院献爱心演出,并在演出后每位乐团成员向儿童们进行“心连心活动”;甲乐团每位成员负责5位小朋友,乙乐团每位成员负责3位小朋友.这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖.请写出所有的抽调方案,并说明理由.
-
科目: 来源: 题型:
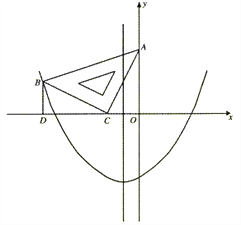
查看答案和解析>>【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C为 (-1,0) .如图所示,B点在抛物线y=
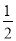 x2+
x2+ x-2图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
x-2图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.(1)求证:△BDC≌△COA;
(2)求BC所在直线的函数关系式;
(3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
相关试题

