【题目】要证明一个三角形中不可能有两个钝角,采用的方法是 ,应先假设
参考答案:
【答案】反证法;一个三角形的三个内角中有两个角是钝角
【解析】解:用反证法证明命题“证明一个三角形中不可能有两个钝角”,采用的方法是:反证法,
应假设“假设一个三角形的三个内角中有两个角是钝角”.
故答案为:一个三角形的三个内角中有两个角是钝角.
根据命题“三角形的内角至多有一个钝角”的否定为“三角形的内角至少有两个钝角”,从而得出结论.
-
科目: 来源: 题型:
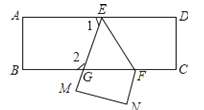
查看答案和解析>>【题目】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G、D、C分别在M、N的位置上,若∠EFG=55°,则∠1=______°,∠2=_______°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.

(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A. a3+a2=a5 B. a3·a2=a5 C. (a3)2=a5 D. a3-a2=a
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于命题“如果a=b,那么ac=bc.”,它的逆命题是________命题.(填“真”或“假”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣x﹣2=0的解是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列推理过程,在括号中填写理由.
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
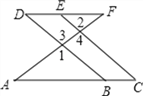
解:∵∠1=∠2(已知),∠1=∠3(______________),
∴∠2=∠3(___________________).
∴__∥__(__________________________________).
∴∠C=∠ABD (________________________________).
又∵∠C=∠D(____________),
∴∠D=∠ABD(等量代换)
∴AC∥DF(______________________________).
相关试题

