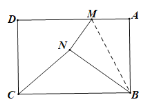
【题目】如图,矩形纸片ABCD中,AD=5,AB=3.若M为射线AD上的一个动点,将△ABM沿BM折叠得到△NBM.若△NBC是直角三角形.则所有符合条件的M点所对应的AM长度的和为______.
参考答案:
【答案】10
【解析】
根据四边形ABCD为矩形以及折叠的性质得到∠A=∠MNB=90°,由M为射线AD上的一个动点可知若△NBC是直角三角形,∠NBC=90°与∠NCB=90°都不符合题意,只有∠BNC=90°.然后分N在矩形ABCD内部与N在矩形ABCD外部两种情况进行讨论,利用勾股定理求得结论即可.
解:∵四边形ABCD为矩形,
∴∠BAD=90°,
∵将△ABM沿BM折叠得到△NBM,
∴∠MAB=∠MNB=90°.
∵M为射线AD上的一个动点,△NBC是直角三角形,
∴∠NBC=90°与∠NCB=90°都不符合题意,
∴只有∠BNC=90°.①当∠BNC=90°,N在矩形ABCD内部,如图1.

∵∠BNC=∠MNB=90°,
∴M、N、C三点共线,
∵AB=BN=3,BC=5,∠BNC=90°,
∴NC=4.
设AM=MN=x,
∵MD=5-x,MC=4+x,
∴在Rt△MDC中,CD2+MD2=MC2,
32+(5-x)2=(4+x)2,
解得x=1;
②当∠BNC=90°,N在矩形ABCD外部时,如图2.

∵∠BNC=∠MNB=90°,
∴M、C、N三点共线,
∵AB=BN=3,BC=5,∠BNC=90°,
∴NC=4,
设AM=MN=y,
∵MD=y-5,MC=y-4,
∴在Rt△MDC中,CD2+MD2=MC2,
32+(y-5)2=(y-4)2,
解得y=9,
则所有符合条件的M点所对应的AM和为1+9=10.
故答案为:10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解本校七年级学生课外阅读的爱好,随机抽取该校七年级部分学生进行问卷调查(每人只选一种书籍)如图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:

(1)这次活动一共调查了多少名学生?
(2)求扇形统计图中“其它”中的扇形圆心角的度数.
(3)补全条形统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP
(2)如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的
 ;
;(3)如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的


-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)5
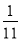 -3
-3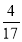 +4
+4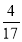 -
-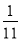
(2)(
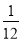 -
-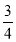 -
-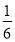 )×(-36)
)×(-36)(3)-
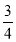 ―(1―0.5)÷
―(1―0.5)÷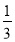 ×[2+(-4)2]
×[2+(-4)2] (4)(
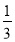 -
-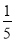 )×52÷|-
)×52÷|-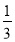 |+(
|+( )2019×42020
)2019×42020 -
科目: 来源: 题型:
查看答案和解析>>【题目】【阅读理解】对于任意正实数a、b,因为
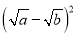 ≥0,所以
≥0,所以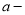
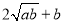 ≥0,所以
≥0,所以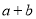 ≥2
≥2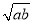 ,只有当
,只有当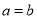 时,等号成立.
时,等号成立.【获得结论】在
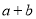 ≥2
≥2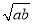 (a、b均为正实数)中,若
(a、b均为正实数)中,若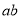 为定值
为定值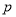 ,则
,则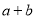 ≥2
≥2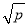 ,只有当
,只有当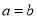 时,
时, 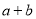 有最小值2
有最小值2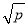 .
.根据上述内容,回答下列问题:若
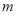 >0,只有当
>0,只有当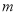 = 时,
= 时, 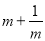 有最小值 .
有最小值 .【探索应用】如图,已知A(-3,0),B(0,-4),P为双曲线
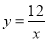 (
(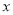 >0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.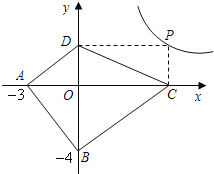
-
科目: 来源: 题型:
查看答案和解析>>【题目】发现问题、探索规律,要有一双敏锐的双眼,下面的图形是由边长为1的小正方形按照某种规律排列而成的.

(1)观察图形,填写下表:
图形个数(n)
(1)
(2)
(3)
正方形的个数
8
图形的周长
18
(2)推测第n个图形中,正方形有 个,周长为 .
(3)写出第30个图形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D,E分别是边BC,AC上的中点,连接DE,并延长DE至点F,使EF=ED,连接AD,AF,BF,CF,线段AD与BF相交于点O,过点D作DG⊥BF,垂足为点G.
(1)求证:四边形ABDF是平行四边形;
(2)当
 时,试判断四边形ADCF的形状,并说明理由;
时,试判断四边形ADCF的形状,并说明理由;(3)若∠CBF=2∠ABF,求证:AF=2OG.

相关试题

