【题目】【阅读理解】对于任意正实数a、b,因为![]() ≥0,所以
≥0,所以![]()
![]() ≥0,所以
≥0,所以![]() ≥2
≥2![]() ,只有当
,只有当![]() 时,等号成立.
时,等号成立.
【获得结论】在![]() ≥2
≥2![]() (a、b均为正实数)中,若
(a、b均为正实数)中,若![]() 为定值
为定值![]() ,则
,则![]() ≥2
≥2![]() ,只有当
,只有当![]() 时,
时, ![]() 有最小值2
有最小值2![]() .
.
根据上述内容,回答下列问题:若![]() >0,只有当
>0,只有当![]() = 时,
= 时, ![]() 有最小值 .
有最小值 .
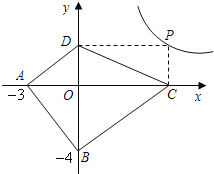
【探索应用】如图,已知A(-3,0),B(0,-4),P为双曲线![]() (
(![]() >0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
参考答案:
【答案】(1)1,2(2)菱形
【解析】分析:(1)根据题目所给信息可知m+![]() ≥2
≥2![]() ,且当m=
,且当m=![]() 时等号成立,可得出答案;
时等号成立,可得出答案;
(2)可设P(x, ![]() ),可表示出AC和BD,则四边形ABCD的面积为S四边形ABCD=2(x+
),可表示出AC和BD,则四边形ABCD的面积为S四边形ABCD=2(x+![]() )+12,再利用所给信息可得到其最小值,此时x=3,可得出AC=BD,可得出四边形ABCD为菱形.
)+12,再利用所给信息可得到其最小值,此时x=3,可得出AC=BD,可得出四边形ABCD为菱形.
详解:(1)根据题目所给信息可知m+![]() ≥2
≥2![]() ,且当m=
,且当m=![]() 时等号,∴当m=1时,m+
时等号,∴当m=1时,m+![]() ≥2,即当m=1时,m+
≥2,即当m=1时,m+![]() 有最小值2.故答案为:1,2;
有最小值2.故答案为:1,2;
(2)设P(x, ![]() ),则C(x,0),D(0,
),则C(x,0),D(0, ![]() ),∴CA=x+3,BD=
),∴CA=x+3,BD=![]() +4,∴S四边形ABCD=
+4,∴S四边形ABCD=![]() CA×BD=
CA×BD=![]() (x+3)(
(x+3)(![]() +4),化简得:S=2(x+
+4),化简得:S=2(x+![]() )+12.∵x>0,
)+12.∵x>0, ![]() >0,∴x+
>0,∴x+![]() ≥2
≥2![]() =6,只有当x=
=6,只有当x=![]() ,即x=3时,等号成立,∴S≥2×6+12=24,∴四边形ABCD的面积有最小值24,此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,∴四边形ABCD是菱形.
,即x=3时,等号成立,∴S≥2×6+12=24,∴四边形ABCD的面积有最小值24,此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,∴四边形ABCD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP
(2)如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的
 ;
;(3)如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的


-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)5
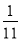 -3
-3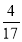 +4
+4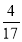 -
-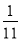
(2)(
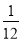 -
-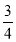 -
-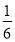 )×(-36)
)×(-36)(3)-
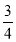 ―(1―0.5)÷
―(1―0.5)÷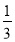 ×[2+(-4)2]
×[2+(-4)2] (4)(
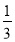 -
-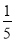 )×52÷|-
)×52÷|-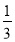 |+(
|+( )2019×42020
)2019×42020 -
科目: 来源: 题型:
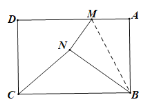
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AD=5,AB=3.若M为射线AD上的一个动点,将△ABM沿BM折叠得到△NBM.若△NBC是直角三角形.则所有符合条件的M点所对应的AM长度的和为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】发现问题、探索规律,要有一双敏锐的双眼,下面的图形是由边长为1的小正方形按照某种规律排列而成的.

(1)观察图形,填写下表:
图形个数(n)
(1)
(2)
(3)
正方形的个数
8
图形的周长
18
(2)推测第n个图形中,正方形有 个,周长为 .
(3)写出第30个图形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D,E分别是边BC,AC上的中点,连接DE,并延长DE至点F,使EF=ED,连接AD,AF,BF,CF,线段AD与BF相交于点O,过点D作DG⊥BF,垂足为点G.
(1)求证:四边形ABDF是平行四边形;
(2)当
 时,试判断四边形ADCF的形状,并说明理由;
时,试判断四边形ADCF的形状,并说明理由;(3)若∠CBF=2∠ABF,求证:AF=2OG.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将若干个奇数按每行8个数排成如图的形式:
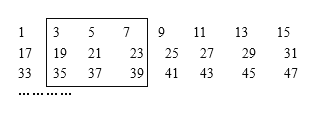
小军画了一方框框住了其中的9个数.
(1)如图中方框内9个数之和是 ;
(2)若小军画的方框内9个数之和等于333,则这个方框内左下角的那个数为_________;
(3)试说明:方框内的9个数之和总是9的倍数.
相关试题

