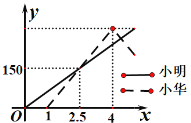
【题目】小明和小华先后从甲地出发到乙地,小明先乘坐客车出发1小时,小华才开车前住乙地,小华到达乙地后立即按原速从乙地返回甲地。已知小明、小华离甲地距离y(千米)与小明出发时间x(小时)之间的函数关系如图所示,请根据图象解答下列问题:小华从乙地返回后再经过___小时与小明相遇.
参考答案:
【答案】![]()
【解析】
设小华从乙地返回后再经过t小时与小明相遇.求出小明和小华的速度及甲地到乙地的路程,根据再次相遇时路程和为甲地到乙地的路程的2倍,列方程求解即可.
设小华从乙地返回后再经过t小时与小明相遇.
小明的速度=150÷2.5=60(千米/时),小华的速度=150÷1.5=100(千米/时),甲地到乙地的路程=100×(4-1)=300(千米).
根据再次相遇时路程和为甲地到乙地的路程的2倍,得:
100(3+t)+60(4+t)=300×2
解得:t=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网络约车公司近期推出了“520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5000个“单次营运里程”数据,这些里程数据均不超过25(千米),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图.
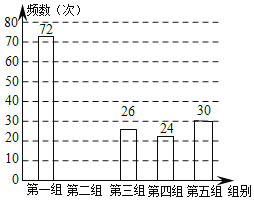
组别
单次营运里程“x”(千米)
频数
第一组
0<x≤5
72
第二组
5<x≤10
a
第三组
10<x≤15
26
第四组
15<x≤20
24
第五组
20<x≤25
30
根据以上信息,解答下列问题:
(1)表中a= ,样本中“单次营运里程”不超过15千米的频率为 ;
(2)请把频数分布直方图补充完整;
(3)估计该公司5000个“单次营运里程”超过20千米的次数.(写出解答过程)
-
科目: 来源: 题型:
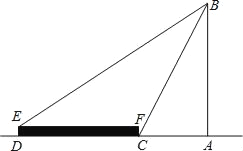
查看答案和解析>>【题目】如图,在一个平台远处有一座古塔,小明在平台底部的点C处测得古塔顶部B的仰角为60°,在平台上的点E处测得古塔顶部的仰角为30°.已知平台的纵截面为矩形DCFE,DE=2米,DC=20米,求古塔AB的高(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】求1+2+22+23+…+22019的值,可令S=1+2+22+23+…+22019,则2S=2+22+23+…+22019+22020因此2S-S=22020-1.仿照以上推理,计算出1+5+52+53+…+52019的值为( )
A. 52019-1B. 52020-1C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入它所属的集合内:
 ,0,5.2,
,0,5.2, 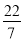 ,+(﹣4),﹣2
,+(﹣4),﹣2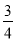 ,﹣(﹣3 ),0.25555…,﹣0.030030003…
,﹣(﹣3 ),0.25555…,﹣0.030030003…(1)分数集合:{______ …}
(2)非负整数集合:{______ …}
(3)有理数集合:{______ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,M、N是对角线BD上两点,且BN=DM.
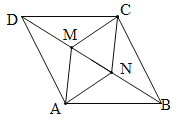
(1)求证:AM=CN;
(2)若AM⊥BD于M,AD=10,CN=6,求DM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“分组合作学习”已成为推动课堂教学改革,打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析,统计图如下:

请结合图中信息解答下列问题:
(1)求出随机抽取调查的学生人数;
(2)补全分组后学生学习兴趣的条形统计图;
(3)分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
相关试题

