【题目】在△ABC中,∠C=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至G,使CG=BF,连接CE、DE、DG.
(1)如图1,求证:四边形CEDG是平行四边形 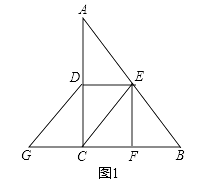 ;
;
(2)如图2,连接EG交AC于点H,若EG⊥AB,请直接写出图2中所有长度等于 ![]() GH的线段.
GH的线段. 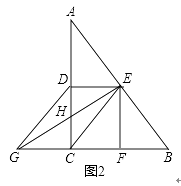
参考答案:
【答案】
(1)证明:如图1中,
∵∠ACB=90°,AE=EB,
∴EC=EA=EB,
∵EF⊥BC,
∴CF=FB,
∵AD=DC,AE=EB,
∴DE∥BC,DE= ![]() BC=BF,
BC=BF,
∵CG=BF,
∴DE=CG,DE∥CG,
∴四边形四边形CEDG是平行四边形
(2)解:如图2中,
∵四边形四边形CEDG是平行四边形,
∴DH=CH,GH=HE,设DH=CH=a,则AD=CD=2a,
∵∠A=∠A,∠AEH=∠ADE=90°,
∴△ADE∽△AEH,
∴AE2=ADAH=2a3a=6a2,
∴AE= ![]() a,
a,
在Rt△AEH中,HE= ![]() =
= ![]() =
= ![]() a,
a,
∴AE= ![]() HE,
HE,
∵GH=HE,AE=EB=CE=CD,
∴线段AE、EB、EC、GD都是线段GH的 ![]() 倍
倍
【解析】(1)欲证明四边形CEDG是平行四边形,只要证明DE∥CG,DE=CG即可.(2)由四边形四边形CEDG是平行四边形,推出DH=CH,GH=HE,设DH=CH=a,则AD=CD=2a,由∠A=∠A,∠AEH=∠ADE=90°,推出△ADE∽△AEH,推出AE2=ADAH=2a3a=6a2 , 推出AE= ![]() a,在Rt△AEH中,HE=
a,在Rt△AEH中,HE= ![]() =
= ![]() =
= ![]() a,推出AE=
a,推出AE= ![]() HE,因为GH=HE,AE=EB=CE=CD,即可推出线段AE、EB、EC、GD都是线段GH的
HE,因为GH=HE,AE=EB=CE=CD,即可推出线段AE、EB、EC、GD都是线段GH的 ![]() 倍.
倍.
【考点精析】关于本题考查的三角形中位线定理和平行四边形的判定与性质,需要了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

-
科目: 来源: 题型:
查看答案和解析>>【题目】张明和李强两名运动爱好者周末相约到东湖绿道进行跑步锻炼.(1)周日早上6点,张明和李强同时从家出发,分别骑自行车和步行到离家距离分别为4.5千米和1.2千米的绿道落雁岛入口汇合,结果同时到达,且张明每分钟比李强每分钟多行220米,求张明和李强的速度分别是多少米/分?
(1)两人到达绿道后约定先跑 6 千米再休息,李强的跑步速度是张明跑步速度的m倍,两人在同起点,同时出发,结果李强先到目的地n分钟.
①当m=12,n=5时,求李强跑了多少分钟?
②张明的跑步速度为 米/分(直接用含m,n的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学为了解该校学生对四种国家一级保护动物的喜爱情况,围绕“在丹顶鹤、大熊猫、滇金丝猴、藏羚羊四种国家一级保护动物中,你最喜欢哪一种动物?(必选且只选一种)”这一问题,在全校范围内随机抽取部分同学进行问卷调查.根据调查结果绘制成如下不完整的条形统计图.其中最喜欢丹顶鹤的学生人数占被抽取人数的16%;请你根据以上信息解答下列问题:

(1)在这次调查中,一共抽取了多少名学生?
(2)求在被调查的学生中,最喜欢滇金丝猴的学生有多少名?并补全条形统计图;
(3)如果全校有1200名学生,请你估计全校最喜欢大熊猫的学生有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为美化校园,计划对面积为1800平方米的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400平方米区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少平方米?
(2)若学校每天付给乙队的绿化费用是0.25万元,每天付给甲队的绿化费用比乙队多60%,要使这次学校付给甲、乙两队的绿化总费用不超过8万元,至少应安排甲队工作多少天? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数x、y满足2x+3y=1.
(1)用含有x的代数式表示y;
(2)若实数y满足y>1,求x的取值范围;
(3)若实数x、y满足x>﹣1,y≥﹣
 ,且2x﹣3y=k,求k的取值范围.
,且2x﹣3y=k,求k的取值范围. -
科目: 来源: 题型:
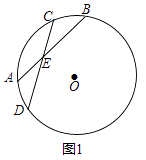
查看答案和解析>>【题目】已知,⊙O的两条弦AB、CD相交于点E,
(1)如图1,若BE=DE,求证: =
= 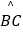 ;
; 
(2)如图2,在(1)的条件下,连接OC,AP为⊙O的直径,PQ为⊙O的弦,且PQ∥AB,求证:∠OCD=∠APQ;
(3)如图3,在(2)的条件下,连接BD分别与OA、OC交于点G、H,连接DQ,设CD与AP交于点F, 若PQ=2CF,BH=5GH,DQ=4,求⊙O的半径.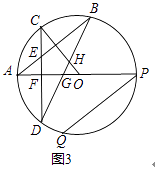
相关试题

