搜索
【题目】已知实数x、y满足2x+3y=1．
（1）用含有x的代数式表示y；
（2）若实数y满足y＞1，求x的取值范围；
（3）若实数x、y满足x＞﹣1，y≥﹣
，且2x﹣3y=k，求k的取值范围．
参考答案：
【答案】（1）y=
；（2）x＜﹣1；（3）﹣5＜k≤4．
【解析】【试题分析】
（1）解关于y的一元一次方程即可；
（2）根据y＞1，将（1）中的式子列成不等式即可；
（3）先解关于x、y的方程组
，再根据x＞﹣1，y≥﹣
，列不等式组即可.
【试题解析】
（1）2x+3y=1，
3y=1﹣2x，
y=
；
（2）y=＞1，
解得：x＜﹣1，
即若实数y满足y＞1，x的取值范围是x＜﹣1；
（3）联立2x+3y=1和2x﹣3y=k得：
，
解方程组得：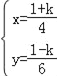
，
由题意得：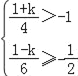
，
解得：﹣5＜k≤4．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市某中学为了解该校学生对四种国家一级保护动物的喜爱情况，围绕“在丹顶鹤、大熊猫、滇金丝猴、藏羚羊四种国家一级保护动物中，你最喜欢哪一种动物？（必选且只选一种）”这一问题，在全校范围内随机抽取部分同学进行问卷调查．根据调查结果绘制成如下不完整的条形统计图．其中最喜欢丹顶鹤的学生人数占被抽取人数的16%；请你根据以上信息解答下列问题：
（1）在这次调查中，一共抽取了多少名学生？
（2）求在被调查的学生中，最喜欢滇金丝猴的学生有多少名？并补全条形统计图；
（3）如果全校有1200名学生，请你估计全校最喜欢大熊猫的学生有多少名？ -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠C=90°，D是AC的中点，E是AB的中点，作EF⊥BC于F，延长BC至G，使CG=BF，连接CE、DE、DG．
（1）如图1，求证：四边形CEDG是平行四边形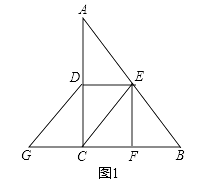
；
（2）如图2，连接EG交AC于点H，若EG⊥AB，请直接写出图2中所有长度等于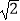
GH的线段．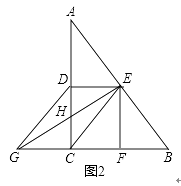 
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校为美化校园，计划对面积为1800平方米的区域进行绿化，安排甲、乙两个工程队完成．已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400平方米区域的绿化时，甲队比乙队少用4天．
（1）求甲、乙两工程队每天能完成绿化的面积分别是多少平方米？
（2）若学校每天付给乙队的绿化费用是0.25万元，每天付给甲队的绿化费用比乙队多60%，要使这次学校付给甲、乙两队的绿化总费用不超过8万元，至少应安排甲队工作多少天？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，⊙O的两条弦AB、CD相交于点E，
（1）如图1，若BE=DE，求证：
= 
； 
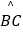（2）如图2，在（1）的条件下，连接OC，AP为⊙O的直径，PQ为⊙O的弦，且PQ∥AB，求证：∠OCD=∠APQ；
（3）如图3，在（2）的条件下，连接BD分别与OA、OC交于点G、H，连接DQ，设CD与AP交于点F， 若PQ=2CF，BH=5GH，DQ=4，求⊙O的半径．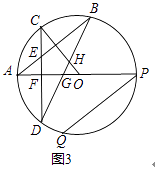
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
-
科目： 来源： 题型：
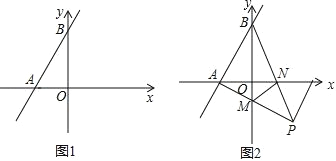
查看答案和解析>>【题目】如图1，在平面直角坐标系中，直线 AB 分别交 x 轴、y 轴于点A（a，0）点 B（0，b），且a、b满足a2+4a+4+|2a+b|＝0
（1）a＝ ；b＝ ．
（2）点 P 在直线AB的右侧，且∠APB＝45°
①若点P在x轴上，则点P的坐标为 ；
②若△ABP 为直角三角形，求点P的坐标；
（2）如图2，在（2）的条件下，点P在第四象限，∠BAP＝90°，AP与y轴交于点M，BP与x轴交于点N，连接MN，求证：MP平分△BMN的一个外角．
相关试题
