【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点

(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= _时,四边形MENF是正方形(只写结论,不需证明)
参考答案:
【答案】解:(1)证明:∵四边形ABCD是矩形,∴∠A=∠D=90°,AB=DC。
又∵MA=MD,∴△ABM≌△DCM(SAS)。
(2)四边形MENF是菱形。证明如下:
∵N、E、F分别是BC、BM、CM的中点,∴NE∥CM,NE=![]() CM,MF=
CM,MF=![]() CM。
CM。
∴NE=FM,NE∥FM。∴四边形MENF是平行四边形。
∵△ABM≌△DCM,∴BM=CM。
∵E、F分别是BM、CM的中点,∴ME=MF。
∴平行四边形MENF是菱形。
(3)2:1
【解析】
试题(1)求出AB=DC,∠A=∠D=90°,AM=DM,根据全等三角形的判定定理推出即可。
(2)根据三角形中位线定理求出NE∥MF,NE=MF,得出平行四边形,求出BM=CM,推出ME=MF,根据菱形的判定推出即可。
(3)当AD:AB=2:1时,四边形MENF是正方形,理由如下:
∵M为AD中点,∴AD=2AM。
∵AD:AB=2:1,∴AM=AB。
∵∠A=90°,∴∠ABM=∠AMB=45°。
同理∠DMC=45°。
∴∠EMF=180°-45°-45°=90°。
∵四边形MENF是菱形,∴菱形MENF是正方形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,点
,点 分别在射线
分别在射线 上移动,
上移动, 的平分线与
的平分线与 的外角平分线交于点
的外角平分线交于点 .
.
(1)当
 时,
时,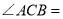 .
.(2)请你猜想:随着
 两点的移动,
两点的移动, 的度数大小是否变化?请说明理由.
的度数大小是否变化?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从2007年4月18日零点起,铁路将实施第六次大提速,届时“子弹头”动力组列车的速度将大大提高.若有一普通列车长为140米,“子弹头”动力组列车长为110米,两列车若同向而行,两车交汇的时间为9秒,若两列车相向而行,两车交汇的时间为3秒,求“子弹头”动力组列车和普通列车的速度分别为多少?若设“子弹头”动力组列车的速度为x米/秒,普通列车速度为y米/秒,则可列出方程组为( )
A.
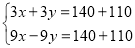 B.
B. 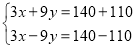
C.
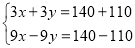 D.
D. 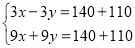
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=10°,点P在OB上.以点P为圆心,OP为半径画弧,交OA于点P1(点P1与点O不重合),连接PP1;再以点P1为圆心,OP为半径画弧,交OB于点P2(点P2与点P不重合),连接P1 P2;再以点P2为圆心,OP为半径画弧,交OA于点P3(点P3与点P1不重合),连接P2 P3;……

请按照上面的要求继续操作并探究:
∠P3 P2 P4=_____°;按照上面的要求一直画下去,得到点Pn,若之后就不能再画出符合要求点Pn+1了,则n=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对x、y定义一种新运算T,记为:T(x,y).
(1)若T(x,y)=x+2y﹣1,如:T(0,1)=0+2×1﹣1=1,则T(1,3)= ;
(2)若T(x,y)=ax+by﹣1,(其中a、b为常数),且T(1,﹣1)=﹣2,T(4,2)=3.
①求a、b的值;
②若关于m的不等式组
 恰好有2个整数解,求实数P的取值范围.
恰好有2个整数解,求实数P的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、AC与⊙O相切于点B、C,∠A=50°,P为⊙O上异于B、C的一个动点,则∠BPC的度数为__________.

相关试题

