【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”,而把1,4,9,16,…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 9=4+5B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】
本题先根据已知条件,得出三角数前面是1,3,6,10,15,21,28,依次差增加1,再从中找出规律,即可找出结果.
解:根据题目中的已知条件结合图象可以得到三角形数是这样的,
三角形数1,3,6,10,15,21,28,后面的数与前面的数的差依次增加1,
正方形数 1 ,4 ,9 ,16 ,25 ,36 ,49,
则25=10+15,36=15+21,49=21+28.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意一个三位数
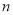 ,如果
,如果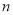 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”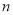 的各个数位上的数字之和记为
的各个数位上的数字之和记为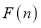 . 例如
. 例如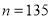 时,
时,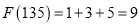 .
. (1)对于“相异数”
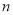 ,若
,若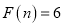 ,请你写出一个
,请你写出一个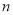 的值;
的值;(2)若
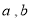 都是“相异数”,其中
都是“相异数”,其中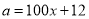 ,
,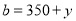 (
(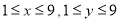 ,
,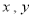 都是正整数),规定:
都是正整数),规定: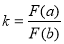 ,当
,当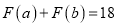 时,求
时,求 的最小值.
的最小值. -
科目: 来源: 题型:
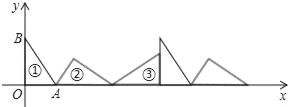
查看答案和解析>>【题目】如图①为Rt△AOB,∠AOB=90°,其中OA=3,OB=4.将AOB沿x轴依次以A,B,O为旋转中心顺时针旋转.分别得图②,图③,…,则旋转到图⑩时直角顶点的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点
 ,
, 为定点,A(2,-3),B(4,-3),定直线
为定点,A(2,-3),B(4,-3),定直线 ,
, 是
是 上一动点,
上一动点, 到AB的距离为6,
到AB的距离为6, ,
, 分别为
分别为 ,
, 的中点,对下列各值:①线段
的中点,对下列各值:①线段 的长度始终为1;②
的长度始终为1;② 的周长固定不变;③
的周长固定不变;③ 的面积固定不变;④若存在点Q使得四边形APBQ是平行四边形,则Q到
的面积固定不变;④若存在点Q使得四边形APBQ是平行四边形,则Q到 所在的直线的距离必为9;其中说法正确的是__(填序号)
所在的直线的距离必为9;其中说法正确的是__(填序号)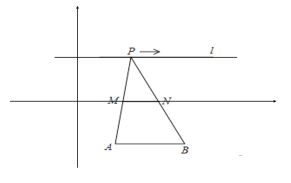
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的一元二次方程
的一元二次方程 .
.(1)求证:方程总有实数根.
(2)设这个方程的两个实数根分别为
 ,
, ,且
,且 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,达到成绩60分及以上为合格,达到90分及以上为优秀,这次竞赛中,甲乙两组学生成绩如下,甲组:30,60,60,60,60,60,70,90,90,100 ;乙组:50,60,60,60,70,70,70,70,80,90.
(1)以上成绩统计分析表中a=______分,b=______分,c=_______分;
组别
平均数
中位数
方差
合格率
优秀率
甲组
68分
a
376
30%
乙组
b
c
90%
(2)小亮同学说:这次竞赛我得了70分,在我们小组中属于中游略偏上,观察上面表格判断,小亮可能是甲乙哪个组的学生?并说明理由
(3)计算乙组的方差和优秀率,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会选择哪一组?并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校九年级学生举行朗诵比赛,全年级学生都参加,学校对表现优异的学生进行表彰,设置一、二、三等奖各进步奖共四个奖项,赛后将九年级(1)班的获奖情况绘制成如图所示的两幅不完整的统计图,请根据图中的信息,解答下列问题:

(1)九年级(1)班共有 名学生;
(2)将条形图补充完整:在扇形统计图中,“二等奖”对应的扇形的圆心角度数是 ;
(3)如果该九年级共有1250名学生,请估计荣获一、二、三等奖的学生共有多少名.
相关试题

