【题目】某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,达到成绩60分及以上为合格,达到90分及以上为优秀,这次竞赛中,甲乙两组学生成绩如下,甲组:30,60,60,60,60,60,70,90,90,100 ;乙组:50,60,60,60,70,70,70,70,80,90.
(1)以上成绩统计分析表中a=______分,b=______分,c=_______分;
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 68分 | a | 376 | 30% | |
乙组 | b | c | 90% |
(2)小亮同学说:这次竞赛我得了70分,在我们小组中属于中游略偏上,观察上面表格判断,小亮可能是甲乙哪个组的学生?并说明理由
(3)计算乙组的方差和优秀率,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会选择哪一组?并说明理由
参考答案:
【答案】(1)60,68,70; (2)甲组,理由见解析;(3)乙组的方差为116,优秀率为10%;选乙组,理由见解析.
【解析】
(1)分别计算甲组的中位数、乙组的平均数和乙组的中位数即可求出a、b、c的值;
(2)从中位数的角度进行说明即可;
(3)根据方差公式计算乙组方差,根据90分以上的人数所占百分比计算乙组的优秀率;因为是选一组同学代表学校参加复赛,所以在两组平均数相同的基础上比较甲乙两组的方差即可得出代表学校参加复赛的小组.
解:(1)![]() ,
,![]() ,
,![]() ,
,
故答案为:60,68,70.
(2)甲组中位数为60,乙组中位数为70,小亮成绩70分位于中上游,属于甲组.
(3)S乙2=![]() =116,优秀率为10%;选择乙组,因为是选一组同学代表学校参加复赛,甲乙平均数一样,但乙的方差小,更稳定,所以选择乙组.
=116,优秀率为10%;选择乙组,因为是选一组同学代表学校参加复赛,甲乙平均数一样,但乙的方差小,更稳定,所以选择乙组.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点
 ,
, 为定点,A(2,-3),B(4,-3),定直线
为定点,A(2,-3),B(4,-3),定直线 ,
, 是
是 上一动点,
上一动点, 到AB的距离为6,
到AB的距离为6, ,
, 分别为
分别为 ,
, 的中点,对下列各值:①线段
的中点,对下列各值:①线段 的长度始终为1;②
的长度始终为1;② 的周长固定不变;③
的周长固定不变;③ 的面积固定不变;④若存在点Q使得四边形APBQ是平行四边形,则Q到
的面积固定不变;④若存在点Q使得四边形APBQ是平行四边形,则Q到 所在的直线的距离必为9;其中说法正确的是__(填序号)
所在的直线的距离必为9;其中说法正确的是__(填序号)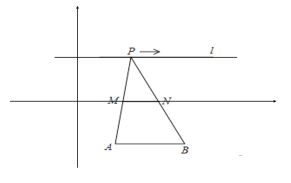
-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”,而把1,4,9,16,…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 9=4+5B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的一元二次方程
的一元二次方程 .
.(1)求证:方程总有实数根.
(2)设这个方程的两个实数根分别为
 ,
, ,且
,且 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校九年级学生举行朗诵比赛,全年级学生都参加,学校对表现优异的学生进行表彰,设置一、二、三等奖各进步奖共四个奖项,赛后将九年级(1)班的获奖情况绘制成如图所示的两幅不完整的统计图,请根据图中的信息,解答下列问题:

(1)九年级(1)班共有 名学生;
(2)将条形图补充完整:在扇形统计图中,“二等奖”对应的扇形的圆心角度数是 ;
(3)如果该九年级共有1250名学生,请估计荣获一、二、三等奖的学生共有多少名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形
 ,对角线
,对角线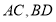 交于点
交于点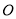 ,点
,点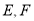 分别是
分别是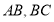 的中点,连接
的中点,连接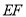 交
交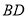 于
于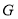 ,连接
,连接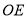
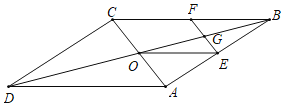
(1)证明:四边形
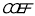 是平行四边形
是平行四边形(2)点
 是哪些线段的中点,写出结论,并选择一组给出证明.
是哪些线段的中点,写出结论,并选择一组给出证明.
相关试题

