搜索
【题目】如图，在ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=4，则AE的长为（ ） 
A.
B.2
C.3
D.4
参考答案：
【答案】B
【解析】解：连结EF，AE与BF交于点O，如图 ∵AB=AF，AO平分∠BAD，
∴AO⊥BF，BO=FO= 
BF=3，
∵四边形ABCD为平行四边形，
∴AF∥BE，
∴∠1=∠3，
∴∠2=∠3，
∴AB=EB，
∵BO⊥AE，
∴AO=OE，
在Rt△AOB中，AO= 
= 
= 
，
∴AE=2AO=2 ．
故选B．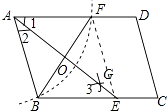
【考点精析】本题主要考查了平行四边形的性质的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品，利用30天的时间销售一种成本为10元/件的商品售后，经过统计得到此商品单价在第x天（x为正整数）销售的相关信息，如表所示：
销售量n（件）
n=50﹣x
销售单价m（元/件）
当1≤x≤20时，m=20+
x当21≤x≤30时，m=10+
（1）请计算第几天该商品单价为25元/件？
（2）求网店销售该商品30天里所获利润y（元）关于x（天）的函数关系式；
（3）这30天中第几天获得的利润最大？最大利润是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在Rt△ABC中，∠ACB=90°，AC=BC，在斜边AB上取一点D，过点D作DE∥BC，交AC于点E，现将△ADE绕点A旋转一定角度到如图2所示的位置（点D在△ABC的内部），使得∠ABD+∠ACD=90°．
（1）①求证：△ABD∽△ACE；
②若CD=1，BD=
，求AD的长．
（2）如图3，将原题中的条件“AC=BC”去掉，其它条件不变，设
= 
=k，若CD=1，BD=2，AD=3，求k的值．
（3）如图4，将原题中的条件“∠ACB=90°”去掉，其它条件不变，若 = = 
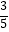，设CD=m，BD=n，AD=p，试探究m，n，p三者之间满足的等量关系．（直接写出结果，不必写出解答过程）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面内直角坐标系中，直线y=2x+4分别交x轴，y轴于点A，C，点D（m，2）在直线AC上，点B在x轴正半轴上，且OB=3OC，点E是y轴上任意一点，记点E为（0，n）．
（1）求点D的坐标及直线BC的解析式；
（2）连结DE，将线段DE绕点D按顺时针旋转90°得线段DG，作正方形DEFG，是否存在n的值，使正方形的顶点F落在△ABC的边上？若存在，求出所有满足条件的n的值；若不存在，说明理由．
（3）作点E关于AC的对称点E′，当n为何值时，AE′分别与AC，BC，AB垂直？ -
科目： 来源： 题型：
查看答案和解析>>【题目】为了求1+3+32+33+…+3100的值，可令M=1+3+32+33+…+3100 ， 则3M=3+32+33+34+…+3101 ， 因此，3M﹣M=3101﹣1，所以M=
，即1+3+32+33+…+3100= ，仿照以上推理计算：1+5+52+53+…+52015的值是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】当前，“校园ipad现象已经受到社会的广泛关注，某教学兴趣小组对”“是否赞成中学生带手机进校园”的问题进行了社会调查．小文将调查数据作出如下不完整的整理： 频数分布表
看法
频数
频率
赞成
5
无所谓
0.1
反对
40
0.8
（1）请求出共调查了多少人；并把小文整理的图表补充完整；
（2）小丽要将调查数据绘制成扇形统计图，则扇形图中“赞成”的圆心角是多少度？
（3）若该校有3000名学生，请您估计该校持“反对”态度的学生人数． -
科目： 来源： 题型：
查看答案和解析>>【题目】学校运动会上，九（1）班啦啦队买了两种矿泉水，其中甲种矿泉水共花费80元，乙种矿泉水共花费60元．甲种矿泉水比乙种矿泉水多买20瓶，且乙种矿泉水的价格是甲种矿泉水价格的1.5倍．求甲、乙两种矿泉水的价格．
相关试题
