【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.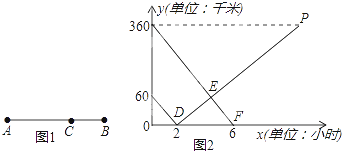
(1)填空:A,B两地相距千米;货车的速度是千米/时.
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数表达式;
(3)客、货两车何时相遇?
参考答案:
【答案】
(1)420,30
(2)解:设2小时后,货车离C站的路程y2与行驶时间x之间的函数表达式为y2=kx+b,根据题意得
360÷30=12(h),12+2=14(h)
∴点P的坐标为(14,360)
将点D(2,0)、点P(14,360)代入y2=kx+b中, ![]()
解得 k=30,b=﹣60
∴y2=30x﹣60
(3)解:设客车离C站的路程y1与行驶时间x之间的函数表达式为y1=k1x+b1,
根据题意得
![]()
解得k1=﹣60,b1=360
y1=﹣60x+360
由y1=y2得
30x﹣60=﹣60x+360
解得x= ![]()
答:客、货两车在出发后 ![]() 小时相遇.
小时相遇.
【解析】根据时间为0时,客车和货车距离C站的距离即可解题,图中给的函数图像和题意可以直接得到A、B两地的距离。
(2)根据题意和函数图像中的数据可以得出两个小时后,货车离C站的路程y2与行驶时间x之间的函数关系式,一般求解函数解析式,利用待定系数法进行求解。
(3)两个函数图像相交,说明两辆车相遇。根据图中的数据分析,利用待定系数法,可求得客车离C站的路程y1与行驶时间x之间的函数解析式,然后令y1=y2,联立得方程,即解得两辆车相遇
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形切去一个角后,形成的另一个多边形的内角和为1 080°,那么原多边形的边数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2﹣25=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
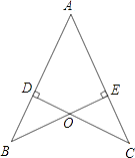
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次知识竞赛中,甲、乙两人进入到“必答题”环节.规则是:两人轮流答题,每人都要回答20道题,每道题回答正确得
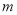 分,回答错误或放弃回答扣
分,回答错误或放弃回答扣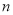 分.当甲、乙两人恰好都答完12道题时,甲答对了9道题,得分为39分;乙答对了10道题,得分为46分.
分.当甲、乙两人恰好都答完12道题时,甲答对了9道题,得分为39分;乙答对了10道题,得分为46分.(1)求
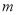 和
和 的值;
的值;(2)规定此环节得分不低于60分能晋级,甲在剩下的比赛中至少还要答对多少道题才能顺利晋级?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形中,两个锐角的差为40°,则这两个锐角的度数分别为__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
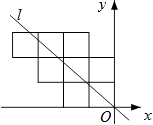
A.y=﹣x
B.y=﹣ x
x
C.y=﹣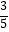 x
x
D.y=﹣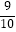 x
x
相关试题

