【题目】如图1,![]() 直线
直线![]() 分别交
分别交![]() 于点
于点![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() 与
与![]() 交于点
交于点![]() 交
交![]() 于
于![]() .
.

(1)求证:![]()
(2)如图2,连接![]() 为
为![]() 上一动点,
上一动点,![]() 平分
平分![]() 交
交![]() 于
于![]() 则
则![]() 的大小是否发生变化?若不变,求出其值;若改变,请说明理由.
的大小是否发生变化?若不变,求出其值;若改变,请说明理由.
参考答案:
【答案】(1)详见解析;(2)![]() 的大小不发生变化,一直是
的大小不发生变化,一直是![]() .
.
【解析】
(1)利用平行线的性质推知![]() ;然后根据角平分线的性质、三角形内角和定理证得
;然后根据角平分线的性质、三角形内角和定理证得![]() ,即
,即![]() ,故结合已知条件
,故结合已知条件![]() ,易证
,易证![]() ;
;
(2)利用三角形外角定理、三角形内角和定理求得![]() ;然后由邻补角的定义、角平分线的定义推知
;然后由邻补角的定义、角平分线的定义推知![]() ;最后根据图形中的角与角间的和差关系求得
;最后根据图形中的角与角间的和差关系求得![]() 的大小不变,是定值
的大小不变,是定值![]() .
.
解:(1)证明:如图1,
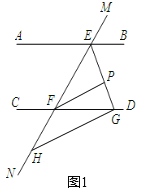
![]() ,
,
![]() .
.
又![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,
,
![]() ,
,
![]() ,即
,即![]() .
.
![]() ,
,
![]() ;
;
(2)![]() 的大小不发生变化,理由如下:
的大小不发生变化,理由如下:
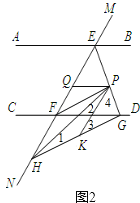
如图2,![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() .
.
![]() 平分
平分![]() ,
,
![]() .
.
∴![]() ,
,
∴![]() 的大小不发生变化,一直是
的大小不发生变化,一直是![]() .
.
-
科目: 来源: 题型:
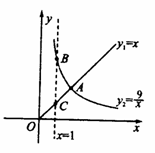
查看答案和解析>>【题目】函数 yl= x ( x ≥0 ) ,
 ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3  时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .
-
科目: 来源: 题型:
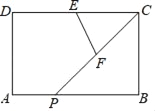
查看答案和解析>>【题目】如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题探究】
已知:如图①所示,∠MPN的顶点为P,⊙O的圆心O从顶点P出发,沿着PN方向平移.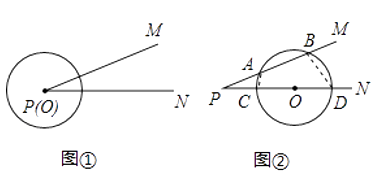
(1)如图②所示,当⊙O分别与射线PM,PN相交于A、B、C、D四个点,连接AC、BD,可以证得△PAC∽△ , 从而可以得到:PAP B=P CP D.
(2)如图③所示,当⊙O与射线PM相切于点A,与射线PN相交于C、D两个点.求证:PA2=PCPD.
(3)【简单应用】
如图④所示,(2)中条件不变,经过点P的另一条射线与⊙O相交于E、F两点.利用上述(1),(2)两问的结论,直接写出线段PA与PE、PF之间的数量关系;当PA=4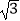 ,EF=2,则PE= .
,EF=2,则PE= . 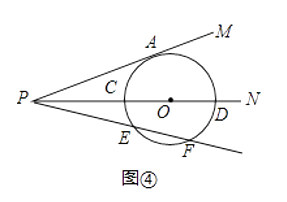
(4)【拓展延伸】如图⑤所示,在以O为圆心的两个同心圆中,A、B是大⊙O上的任意两点,经过A、B 两点作线段,分别交小⊙O于C、E、D、F四个点.求证:ACAE=BDBF.(友情提醒:可直接运用本题上面所得到的相关结论)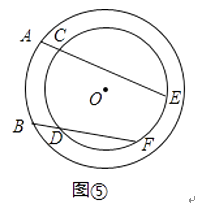
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=﹣
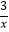 ,下列结论不正确的是( )
,下列结论不正确的是( )
A.图象必经过点(﹣1,3)
B.若x>1,则﹣3<y<0
C.图象在第二、四象限内
D.y随x的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是﹣1,则顶点A坐标是( )
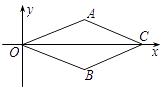
A.(2,1)
B.(1,﹣2)
C.(1,2)
D.(2,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了适应广大市民锻炼,休闲的需要,某市新修建了一条绿道
 (如图),父子两人同时从起点
(如图),父子两人同时从起点 出发,沿绿道进行跑步锻炼,到达
出发,沿绿道进行跑步锻炼,到达 点后立即返回向起点
点后立即返回向起点 跑去,他们不断往返于
跑去,他们不断往返于 之间,已知父子两人的速度分别为2米/秒和3米/秒,儿子第一次到达
之间,已知父子两人的速度分别为2米/秒和3米/秒,儿子第一次到达 点时,父亲离
点时,父亲离 点还有1200米,则(1)父亲第一次到达
点还有1200米,则(1)父亲第一次到达 点时,儿子离
点时,儿子离 点的距离是_________米;(2)从起点
点的距离是_________米;(2)从起点 出发后________小时父子两人恰好第一次同时回到起点
出发后________小时父子两人恰好第一次同时回到起点 .
.
相关试题

