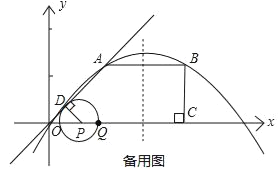
【题目】如图,O是平面直角坐标系的原点.在四边形OABC中,AB∥OC,BC⊥x轴于C,A(1,1),B(3,1),动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.设P点运动的时间为t秒(0<t<2).
(1)求经过O、A、B三点的抛物线的解析式;
(2)过P作PD⊥OA于D,以点P为圆心,PD为半径作⊙P,⊙P在点P的右侧与x轴交于点Q.
①则P点的坐标为_____,Q点的坐标为_____;(用含t的代数式表示)
②试求t为何值时,⊙P与四边形OABC的两边同时相切;
③设△OPD与四边形OABC重叠的面积为S,请直接写出S与t的函数解析式.

参考答案:
【答案】 (2t,0) ((2+![]() )t,0)
)t,0)
【解析】分析:(1)利用待定系数法即可得出结论;
(2)①先用含t的代数式表示出OP,再利用锐角三角函数表示出PD,进而表示出OQ即可得出结论;
②分⊙P与AB相切时,⊙P与BC相切时两种情况,利用直线和圆相切的性质建立方程求解即可;
③分0<t≤1,1<t≤![]() ,
,![]() <t<2三种情况,利用几何图形的面积公式即可得出结论.
<t<2三种情况,利用几何图形的面积公式即可得出结论.
详解:(1)因为抛物线经过原点O,所以设抛物线解析式为y=ax2+bx.
又因为抛物线经过A(1,1),B(3,1),
所以有![]() 解得
解得![]() ,
,
所以抛物线解析式为y=﹣![]() x2+
x2+![]() x
x
(2)①由运动知,OP=2t,
∴P(2t,0),
∵A(1,1),
∴∠AOC=45°,
∵PD⊥OA,
∴PD=OPsin∠AOC=![]() t,
t,
∵PD为半径作⊙P,⊙P在点P的右侧与x轴交于点Q,
∴PQ=PD=![]() t,
t,
∴OQ=OP+PQ=2t+![]() t=(2+
t=(2+![]() )t
)t
∴Q((2+![]() )t,0),
)t,0),
故答案为(2t,0),((2+![]() )t,0);
)t,0);
②当⊙P与AB相切时,![]() t=1,所以t=
t=1,所以t=![]() ;
;
当⊙P与BC相切时,即点Q与点C重合,所以(2+![]() )t=3,解得t=
)t=3,解得t=![]() .
.
(3)①当0<t≤1,如图1,重叠部分的面积是S△OPQ,
过点A作AF⊥x轴于点F,
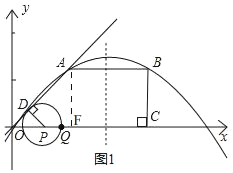
∵A(1,1),
在Rt△OAF中,AF=OF=1,∠AOF=45°,
在Rt△OPQ中,
∴PQ=OQ=2tcos45°=![]() t,
t,
∴S=![]() (
(![]() t)2=t2,
t)2=t2,
②当1<t≤![]() ,如图2,设PQ交AB于点G,
,如图2,设PQ交AB于点G,
作GH⊥x轴于点H,∠OPQ=∠QOP=45°,
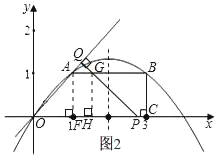
则四边形OAGP是等腰梯形,PH=GH=AF=1,
重叠部分的面积是S梯形OAGP.
∴AG=FH=OP﹣PH﹣OF=2t﹣2,
∴S=(AG+OP)AF=![]() (2t+2t﹣2)×1=2t﹣1.
(2t+2t﹣2)×1=2t﹣1.
③当![]() <t<2,如图3,设PQ与AB交于点M,交BC于点N,
<t<2,如图3,设PQ与AB交于点M,交BC于点N,
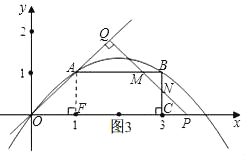
重叠部分的面积是S五边形OAMNC.
因为△PNC和△BMN都是等腰直角三角形,
所以重叠部分的面积是S五边形OAMNC=S梯形OABC﹣S△BMN.
∵B(3,1),OP=2t,
∴CN=PC=OP﹣OC=2t﹣3,
∴BM=BN=1﹣(2t﹣3)=4﹣2t,
∴S=![]() (2+3)×1﹣
(2+3)×1﹣![]() (4﹣2t)2=﹣2t2+8t﹣
(4﹣2t)2=﹣2t2+8t﹣![]() .
.
即:S=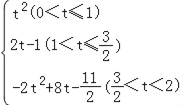 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,对角线AC,BD相交于点O.EF过点O且与ABCD分别相交于点E,F
(1)如图①,求证:OE=OF;
(2)如图②,若EF⊥DB,垂足为O,求证:四边形BEDF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有两点A、B,点B在点A的右侧,且AB=10,点A表示的数为﹣6.动点P从点A出发,以每秒4个单位长度的速度沿数轴向右匀速运动.
(1)写出数轴上点B表示的数;
(2)经过多少时间,线段AP和BP的长度之和为18?
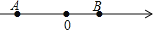
-
科目: 来源: 题型:
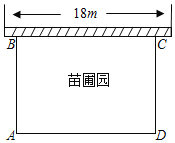
查看答案和解析>>【题目】某中学课外兴趣活动小组准备围建一个矩形的苗圃圆.其中一边靠墙,另外三边用长为40m的篱笆围成.已知墙长为18m(如图所示),设这个苗圃园垂直于墙的一边AB为xm
(1)用含有x的式子表示AD,并写出x的取值范围;
(2)若苗圃园的面积为192m2平方米,求AB的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3),动点F从点O出发以每秒1个单位长度的速度沿OC向终点C运动,运动
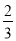 秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)
秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)(1)OE= ,OF= (用含t的代数式表示)
(2)当t=1时,将△OEF沿EF翻折,点O恰好落在CB边上的点D处
①求点D的坐标及直线DE的解析式;
②点M是射线DB上的任意一点,过点M作直线DE的平行线,与x轴交于N点,设直线MN的解析式为y=kx+b,当点M与点B不重合时,S为△MBN的面积,当点M与点B重合时,S=0.求S与b之间的函数关系式,并求出自变量b的取值范围.

-
科目: 来源: 题型:
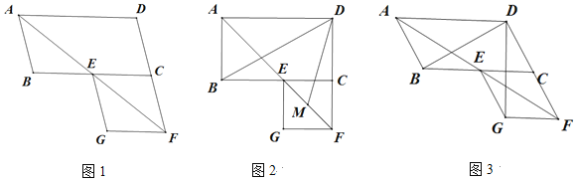
查看答案和解析>>【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 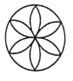
相关试题

