【题目】下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A.  B.
B. 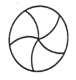 C.
C. 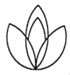 D.
D. 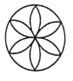
参考答案:
【答案】D
【解析】分析:中心对称图形是:在平面内,一个图形经过中心对称能与原来的图形重合,这个图形叫做叫做中心对称图形。轴对称图形是:一个图形的一部分,以某条直线为对称轴,经过轴对称能与图形的另一部分重合,这样的图形叫做轴对称图形.
详解:A. 不是轴对称图形,是中心对称图形,故不正确;
B. 既不是轴对称图形也不是中心对称图形,故不正确;
C. 是轴对称图形,不是中心对称图形,故不正确;
D. 既是轴对称图形又是中心对称图形,故正确;
故选D.
点睛:本题考查了轴对称图形和中心对称图形的识别,熟记轴对称图形和中心对称图形的定义是解答本题的关键.
-
科目: 来源: 题型:
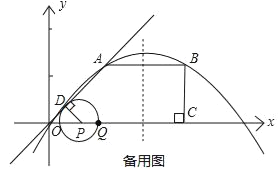
查看答案和解析>>【题目】如图,O是平面直角坐标系的原点.在四边形OABC中,AB∥OC,BC⊥x轴于C,A(1,1),B(3,1),动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.设P点运动的时间为t秒(0<t<2).
(1)求经过O、A、B三点的抛物线的解析式;
(2)过P作PD⊥OA于D,以点P为圆心,PD为半径作⊙P,⊙P在点P的右侧与x轴交于点Q.
①则P点的坐标为_____,Q点的坐标为_____;(用含t的代数式表示)
②试求t为何值时,⊙P与四边形OABC的两边同时相切;
③设△OPD与四边形OABC重叠的面积为S,请直接写出S与t的函数解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3),动点F从点O出发以每秒1个单位长度的速度沿OC向终点C运动,运动
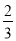 秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)
秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)(1)OE= ,OF= (用含t的代数式表示)
(2)当t=1时,将△OEF沿EF翻折,点O恰好落在CB边上的点D处
①求点D的坐标及直线DE的解析式;
②点M是射线DB上的任意一点,过点M作直线DE的平行线,与x轴交于N点,设直线MN的解析式为y=kx+b,当点M与点B不重合时,S为△MBN的面积,当点M与点B重合时,S=0.求S与b之间的函数关系式,并求出自变量b的取值范围.

-
科目: 来源: 题型:
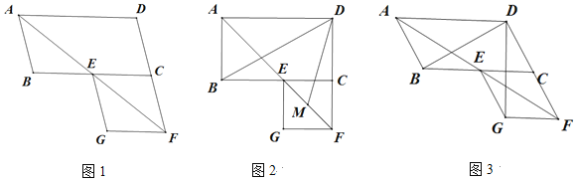
查看答案和解析>>【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
-
科目: 来源: 题型:
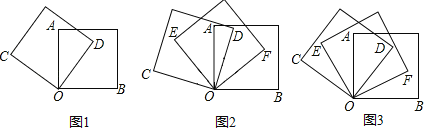
查看答案和解析>>【题目】已知正方形的每个角等于90°,请解决下列问题:
(1)如图1,将两个正方形的一个顶点O重合放置,若∠AOD=50°,求∠COB的度数;
(2)如图2,将三个正方形的一个顶点O重合放置,若∠EOC=40°,∠BOF=30°,求∠AOD的度数;
(3)如图3,将三个正方形的一个顶点O重合放置,若OF平分∠DOB,那么OE平分∠AOC吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面上
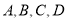 四个点.
四个点. 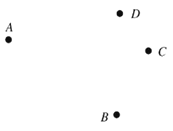
(1)按下列要求画图(不写画法)
①连接
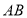 ,
,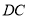 ;②作直线
;②作直线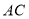 ;③作射线
;③作射线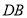 ,交
,交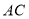 于点
于点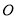 .
. (2)在(1)所画的图形中共有__________条线段,__________条射线. (所画图形中不能再添加标注其他字母);
(3)通过测量线段
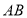 ,
,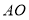 ,
,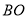 ,可知
,可知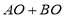 __________
__________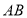 (填“
(填“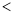 ”,“
”,“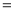 ”或“
”或“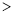 ”),可以解释这一现象的基本事实为:_______________________.
”),可以解释这一现象的基本事实为:_______________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=
 BD
BD其中正确结论的为______(请将所有正确的序号都填上).

相关试题

