【题目】已知:如图,点E,F分别在AB,CD上,AF⊥CE,垂足为点O,∠1=∠B,
∠A+∠2=90°.求证:AB∥CD.
证明:如图,
∵∠1=∠B(已知)
∴CE∥BF(同位角相等,两直线平行)
______________
∴∠AFC+∠2=90°(等式性质)
∵∠A+∠2=90°(已知)
∴∠AFC=∠A(同角或等角的余角相等)
∴AB∥CD(内错角相等,两直线平行)
请你仔细观察下列序号所代表的内容:
①∴∠AOE=90°(垂直的定义)
②∴∠AFB=90°(等量代换)
③∵AF⊥CE(已知)
④∵∠AFC+∠AFB+∠2=180°(平角的定义)
⑤∴∠AOE=∠AFB(两直线平行,同位角相等)
横线处应填写的过程,顺序正确的是( )
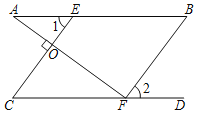
A.⑤③①②④B.③④①②⑤C.⑤④③①②D.⑤②④
参考答案:
【答案】A
【解析】
先证CE∥BF得∠AOE=∠AFB,由AF⊥CE得∠AOE=∠AFB=90°,利用平角定义得出∠AFC+∠2=90°,结合∠A+∠2=90°可以得出∠AFC=∠A,从而得证.
证明:如图,
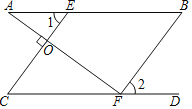
∵∠1=∠B(已知)
∴CE∥BF(同位角相等,两直线平行)
⑤∴∠AOE=∠AFB(两直线平行,同位角相等)
③∵AF⊥CE(已知)
①∴∠AOE=90°(垂直的定义)
②∴∠AFB=90°(等量代换)
④∵∠AFC+∠AFB+∠2=180°(平角的定义)
∴∠AFC+∠2=90°(等式性质)
∵∠A+∠2=90°(已知)
∴∠AFC=∠A(同角或等角的余角相等)
∴AB∥CD(内错角相等,两直线平行),
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图所示,这是某校八(1)班教室简图,点
 、
、 、
、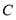 、
、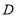 、
、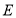 分别代表五个学习小组的位置.已知
分别代表五个学习小组的位置.已知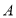 点的坐标为(-1,3).
点的坐标为(-1,3).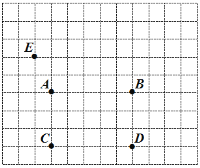
(1)请按题意建立平面直角坐标系(横轴和纵轴均为小正方形的边所在直线,每个小正方形边长为1个单位长度),写出图中其他几个学习小组的坐标;
(2)若(1)中建立的平面直角坐标系坐标原点为
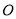 ,点
,点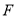 在
在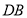 的延长线上,请写出
的延长线上,请写出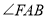 、
、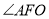 、
、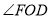 之间的等量关系,并说明原因.
之间的等量关系,并说明原因. -
科目: 来源: 题型:
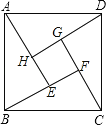
查看答案和解析>>【题目】如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为_____.
-
科目: 来源: 题型:
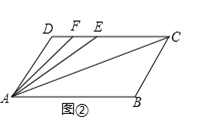
查看答案和解析>>【题目】如图①,已知AD∥BC,∠B=∠D=120°.
(1)请问:AB与CD平行吗?为什么?
(2)若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.
(3)若点E在直线CD上,且满足∠EAC=
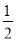 ∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).
∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).
-
科目: 来源: 题型:
查看答案和解析>>【题目】珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=__________度.

(第22题)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,按以下步骤作图:①分别以点A和点C为圆心,以大于
 AC的长为半径作弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD.若AB=BD,AB=6,∠C=30°,则△ACD的面积为_____.
AC的长为半径作弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD.若AB=BD,AB=6,∠C=30°,则△ACD的面积为_____.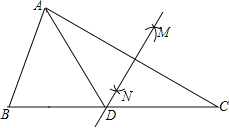
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组
(1)用代入法解方程组
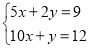
(2)用加减法解方程组
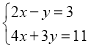
(3)解方程组
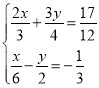
(4)解方程组
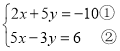
相关试题

